Фигуры и тела |
Линейные преобразованияРассмотрим тень, отбрасываемую на солнце вырезанной из картона фигурой F на плоскость а, не обязательно параллельную этой фигуре (рис. 20). Геометрически переход от фигуры F к ее тени F' описывают как параллельное проектирование, переводящее каждую точку А фигуры F в такую точку А' плоскости а, что АА'||а, где а - \заданная прямая, характеризующая направление проектирования (ибо лучи солнца можно считать параллельными). 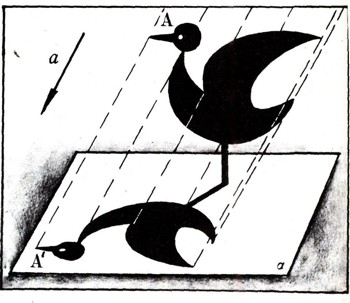 Рис. 20.
Фигура F' может значительно отличаться от первоначальной фигуры F; так, каждый знает, насколько сильно искажены на тени истинная форма и размеры предметов, если солнце стоит достаточно низко (рис. 21). Однако некоторое сходство между фигурой F и ее тенью F' и тут сохранится. Так, например, каждая прямая, проведенная в плоскости фигуры F, перейдет снова в прямую линию (рис. 22); параллельные прямые перейдут в параллельные прямые; отношение длин отрезков, принадлежащих одной прямой (но не разным прямым!), при параллельном проектировании сохранится (см. рис. 22, где AB/BC=A'B'/B'?') Квадрат параллельное проектирование уже не переведет в квадрат; однако оно переведет его в параллелограмм, который отличается от квадрата не так уж резко.  Рис. 21.
Геометрические преобразования, обладающие такими свойствами, называются линейными преобразованиями. К числу линейных преобразований относится, например, так называемое сжатие к прямой l, которое описывается так: точку А плоскости сжатие к прямой l переводит в такую точку А', что точки А и А' лежат на одном перпендикуляре к прямой l и PA'/PA = k, где Р - основание перпендикуляра (рис. 23). Постоянное число k называется коэффициентом сжатия к прямой (при k > 1 было бы правильнее говорить о "растяжении" от прямой l). Нетрудно убедиться, что сжатие к прямой также переводит прямую линию снова в прямую; параллельные прямые переводит в параллельные; сохраняет отношения длин отрезков, принадлежащих одной прямой. 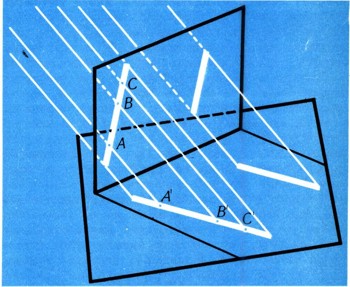 Рис. 22 Параллельное проектирование.
Знание свойств, сохраняющихся при линейных преобразованиях, позволяет использовать эти преобразования для доказательства некоторых геометрических теорем. Разумеется, квадрат ABCD и получающийся из него параллельным проектированием параллелограмм A'B'C'D' имеют много разных свойств; однако те свойства, которые сохраняются при линейных преобразованиях, совпадают у квадрата и у параллелограмма. Выберем произвольную точку Е на диагонали АС квадрата ABCD и проведем через нее отрезки MN||AB и PQ||BC (рис. 24,a). Нетрудно видеть, что прямая АС явится осью симметрии полученного чертежа; поэтому прямые MQ и PN (симметричные относительно прямой AС!) пересекутся на прямой АС. А отсюда вытекает, что и отрезки M'N'||A'B' и P'Q'||B'C', пересекающиеся на диагонали А'С' параллелограмма A'B'C'D', отсекают от параллелограмма меньшие параллелограммы M'D'Q'E' и N'B'P'E', диагонали M'Q' и P'N' которых пересекаются на прямой А'С' (рис. 24, б). Доказать это, не пользуясь линейными преобразованиями, было бы затруднительно! 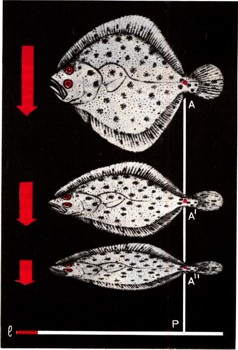 Рис. 23 Сжатие к прямой.
Рассмотрим еще и такой пример. Ясно, что каждый треугольник ABC можно параллельным проектированием перевести в равносторонний треугольник ABC' (рис. 25; треугольники ABC' и ABC расположены в разных плоскостях; СС' - направление проектирования). При этом медианы треугольника ABC переходят в медианы треугольника ABC' (это следует из свойств параллельного проектирования). Но медианы равностороннего треугольника являются одновременно и биссектрисами; поэтому они пересекаются в одной точке - центре окружности, вписанной в треугольник ABC'. А отсюда следует, что также и медианы, исходного треугольника ABC пересекаются в одной точке. Это доказательство теоремы о точке пересечения медиан треугольника является, вероятно, простейшим! 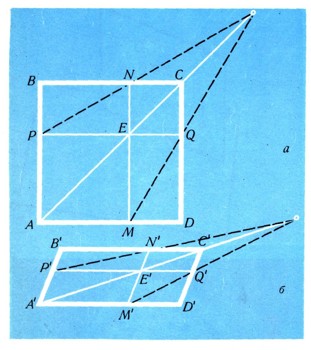 Рис. 24.
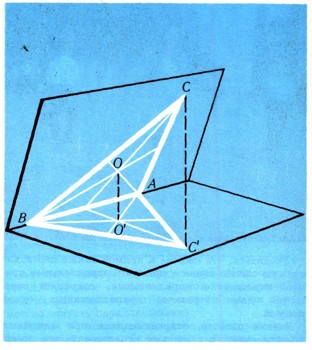 Рис. 25.
|
 |