Фигуры и тела |
Как применяется геометрическая теорияИтак, в геометрии изучаются свойства абстрактных понятий - точки, прямой, плоскости. Эти свойства формулируются и доказываются в так называемых теоремах. Доказательство же всех теорем основано в конечном счете на некоторых аксиомах, которые никак не доказываются. Подробнее о том, как выбираются аксиомы, каким требованиям должен удовлетворять этот выбор, рассказано в статье "Как возникла геометрия". Наиболее ранняя из дошедших до нас систем аксиом была построена Евклидом (III в. до н. э.). Аксиоматика (система аксиом), данная Евклидом, была, правда, далеко не безупречной. Строгое современное изложение евклидовой геометрии было дано лишь в конце XIX в.; оно базируется на двух десятках аксиом, которые мы здесь перечислять не будем. Все теоремы геометрии лишь с той точностью описывают реальный мир, с какой аксиомы правильно отражают действительное положение вещей.  Рис. 3. Со старинной гравюры.
Существо дела заключается в следующем. Пусть, например, мы 'рассматриваем распространение света в природе, так сказать "световые лучи". Они ведут себя в соответствии с действующими физическими законами. И вот геометры-математики выбирают некоторые обнаруженные в опытах особенности распространения света и объявляют их аксиомами, присущими абстрактным понятиям точки, прямой, плоскости. На базе выбранных аксиом и строят математическую науку геометрию. Эта геометрия является как бы мысленным слепком с действительного мира. Изучение этого слепка позволяет обнаруживать закономерности реального мира уже не путем непосредственных измерений, а мысленно, геометрически (т. е. на слепке). 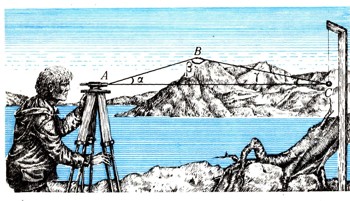 Рис. 4. Измерение расстояния между пунктами А и В,
разделенными рекой.
Чтобы подробнее пояснить это, рассмотрим, например, задачу об определении расстояния между пунктами А и В, разделенными рекой (рис. 4). Понятно, что прямое измерение расстояния А В практически неосуществимо. (Еще труднее найти расстояние между звездами.) Для решения подобных задач необходима геометрия. Как же найти расстояние АВ с помощью геометрии? Укажем два способа решения этой задачи. 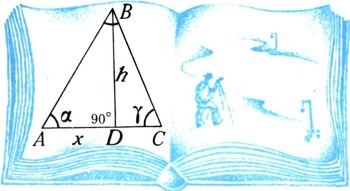 Рис. 5
Первый способ Выберем на местности еще один пункт С так, чтобы расстояние АС можно было непосредственно измерить. Найдя АС, измерим с помощью какого-либо угломерного инструмента (скажем, теодолита) поочередно углы а и y (положим для определенности, что они оказались острыми). Теперь, уже мысленно, рассмотрим абстрактный треугольник АВС, У которого задана сторона АС и углы а и у. Мы можем для наглядности нарисовать этот треугольник (рис. 5), хотя никакой необходимости в этом нет; все дальнейшие рассуждения можно проводить мысленно, не обращаясь к рисунку. Поэтому и рисунок, если уж его желательно сделать, может быть выполнен приблизительно, без соблюдения каких-либо чертежных правил. Опуская из вершины В перпендикуляр на сторону АС, получим точку D. Обозначим BD = h, AD = x. Тогда DC=AC-x. Очевидно, 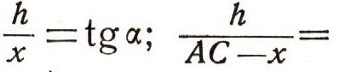
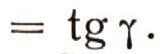 Отсюда 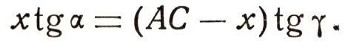 Следовательно, 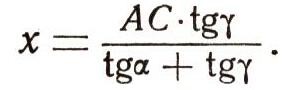 После этого по теореме Пифагора легко найдем: 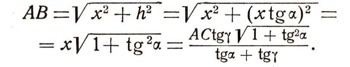 Зная АС, а, у, можно по полученной формуле легко найти искомое расстояние АВ. (Расстояние АВ можно найти еще проще, если воспользоваться известной в тригонометрии теоремой синусов.) Постараемся на бумаге по возможности точно начертить план местности (план треугольника ABC). Разумеется, невозможно начертить его в натуральную величину. Поэтому выберем определенный масштаб и уменьшим измеренную величину АС в п раз. Построим на чертеже отрезок А'С'=1/n* АС. Далее, на концах этого отрезка с помощью транспортира построим углы а и у. В пересечении сторон этих углов получим точку В' -третью вершину треугольника. Так как два угла а и y треугольника А'В'С' равны соответствующим углам треугольника ABC, то эти треугольники подобны. А так как подобие треугольников означает пропорциональность их соответствующих сторон, то приходим к выводу, что сторона А'В' должна быть меньше стороны АВ также в п раз. Поэтому, зная длину А'В', можно найти АВ = пА'В'. В первом случае мы нашли АВ простым вычислением, во втором пришлось выполнить достаточно точный чертеж. В обоих случаях для определения АВ нам пришлось воспользоваться теоремами геометрии: теоремой Пифагора, теоремой о свойстве подобных треугольников и т. п. Отметим, что второй способ (наряду с первым) часто используется в инженерной практике, где поэтому весьма важным является точное выполнение чертежей. Можно ли гарантировать, что описанные методы дают величину АВ, которая с необходимой точностью совпадает с расстоянием между пунктами А и В, если бы его действительно удалось измерить? Ответ на этот вопрос зависит от того, насколько точно аксиомы геометрии (а следовательно, и теоремы) отображают реальную действительность, насколько хорош наш геометрический слепок с реального мира. Разумеется, может оказаться, что этот слепок недостаточно хорош. Тогда надо попытаться сделать лучший. Для этого нужно тщательнее проанализировать опыты, на основании которых выбраны те или иные аксиомы, - точнее, выбрать аксиомы. С помощью новых аксиом, более точно отображающих действительность, надо построить новую геометрию, новый, более точный слепок с реального мира. В течение двух тысячелетий считалось, что евклидова геометрия описывает мир с беспредельной точностью, что евклидов слепок с реального мира идеален. Эта точка зрения была впервые поколеблена лишь в 1826 г. русским математиком Н. И. Лобачевским. Чтобы разъяснить его идеи, остановимся подробно на анализе одной из самых интересных аксиом евклидовой геометрии. |
 |