Функции |
ПрямаяПрямая - это простейшая из линий; уравнение первой степени - простейшее из уравнений. И вот оказывается, что: 1) всякая прямая линия задается некоторым уравнением первой степени и 2) все точки, удовлетворяющие заданному уравнению первой степени относительно х и у, заполняют некоторую прямую, т. е. такое уравнение и служит уравнением прямой. Докажем две теоремы. 1. Уравнение всякой прямой есть уравнение первой степени.. Прежде всего это ясно для прямой, параллельной оси Оу (в частности, и для самой оси Оу), так как у всех точек такой прямой абсцисса одна и та же, т. е. равна некоторому постоянному а; х = а - это и есть уравнение рассматриваемой прямой, но оно первой степени. Рассмотрим теперь любую прямую п, не параллельную Оу. Она пересекает Оу в некоторой точке В (0; b) (абсцисса точки В равна нулю, а ордината имеет некоторое значение b). Передвинем прямую п параллельно себе так, чтобы она прошла через начало О (0; 0). Составим прежде всего уравнение этой вспомогательной прямой. На ней найдется точка Е (рис. 11) с абсциссой, равной 1 (точка ее пересечения с прямой x = 1); пусть ордината точки Е равна числу k: Е (1; k). Тогда для любой точки этой прямой y:x = k:1. Действительно, треугольники ОМ1M и ОЕ1Е подобны, поэтому их катеты |y|, |х, |k|, 1 пропорциональны: |y|:|x|=|k|::l. Остается проверить лишь знаки: чертеж показывает, что если k положительно, то для любой точки прямой ЕО непременно х и у будут или оба положительны, или оба отрицательны. Значит, одинаковы и знаки отношений у:х, k:1. Если k отрицательно, то знаки х и у противоположны (рис. 12) и равенство y:x = k:1, или y=kx, остается в силе. При k = 0 точка Е лежит на оси Ох, прямая ОЕ совпадает с осью Ох, а уравнение y=kx превращается в y = 0. Итак, при любом k уравнением прямой ОЕ служит равенство y = kx. 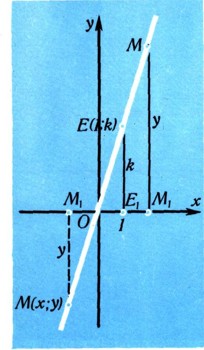 Рис. 11.
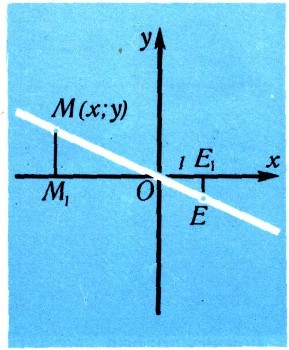 Рис. 12.
Вернемся теперь к первоначальной прямой п; ее можно получить из вспомогательной прямой ОЕ сдвигом в направлении оси Оу на отрезок b. Это значит, что каждая ее точка перемещается в направлении оси Оу на b (если b>0 - вверх, если b<0 -вниз). Ордината каждой точки при этом изменится на одно и то же число b, а абсцисса останется прежней; вместо уравнения y=kx вспомогательной прямой мы теперь получим: 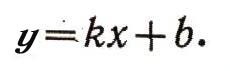 Это и будет уравнением прямой п. (Напомним, что ни одна чужая точка этому уравнению не удовлетворяет: для точек, лежащих выше нашей прямой, y>kx + b; для точек, лежащих ниже, y<kx+b; число k называется угловым коэффициентом прямой, b - начальной ординатой.) Из треугольника ОЕЕ1 легко выяснить геометрический смысл углового коэффициента прямой: это тангенс угла, который наша прямая образует с положительным направлением оси Ох. Если угол тупой, то k отрицательно. 2. Всякое уравнение первой степени 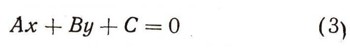 есть уравнение некоторой прямой. Действительно, А и В сразу оба не могут быть равны нулю (так как тогда наше уравнение не было бы уравнением первой степени). Пусть, например, 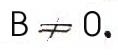 тогда уравнение можно разрешить относительно у; оно примет вид: 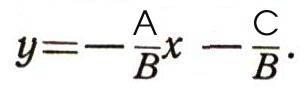 Если теперь построить прямую с угловым коэффициентом k, равным 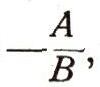 и начальной ординатой b, равной 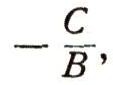 то, как мы уже видели, ее уравнение будет: y = kx + b, или 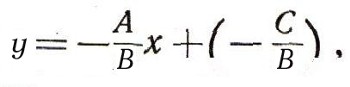 оно равносильно заданному. (Случай В = 0, А не равно 0 приведет к уравнению 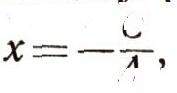 т. е. х постоянно. Это уравнение прямой, параллельной оси Оу; при С = 0 - сама ось Оу.) |
 |