Интеграл и производная |
Применение интеграловМы научились вычислять интегралы от многочленов. Этого уже достаточно, чтобы иметь возможность решать многие математические и физические задачи. Покажем для начала, как просто получаются с помощью интегралов некоторые формулы, изучаемые в школе. Выведем формулу пути равноускоренного движения. Если начальная скорость тела в момент t=0 равна v0, а ускорение движения равно а, то в момент времени t скорость тела составит v(t)=v0+at. Поэтому по формуле (3) путь, пройденный телом с начала движения до момента Т, выражается формулой: 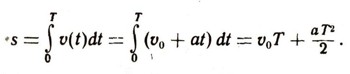 Выведем теперь некоторые геометрические формулы. Сначала найдем, чему равен объем шара радиуса R. Конечно, нам достаточно найти объем полушара, а потом его удвоить. Рассечем полушар плоскостью, параллельной его основанию и отстоящей на х от основания (рис. 14). В сечении получится круг радиуса 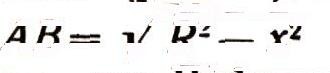
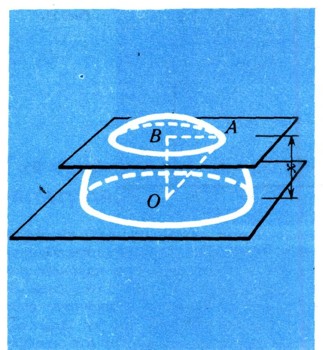 Рис. 14.
(это получается, если применить теорему Пифагора к треугольнику ОАВ). Поэтому площадь получившегося сечения равна: 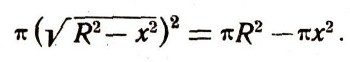 Но тогда объем полушара (высота его равна R) выражается формулой: 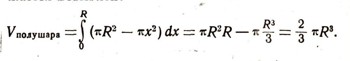 Следовательно, объем всего шара равен 4/3Пи*R3. Но с помощью интегрального исчисления можно найти и такие площади и объемы, которые не изучаются в школе. Найдем, например, площадь параболического сегмента АОВА, у которого хорда АВ равна b, а стрелка ОС равна h (рис. 15). Уравнение параболы имеет вид у=ах2. В точке с абсциссой х=b/2 ордината AD должна равняться длине стрелки h. Поэтому 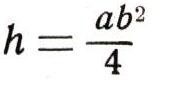
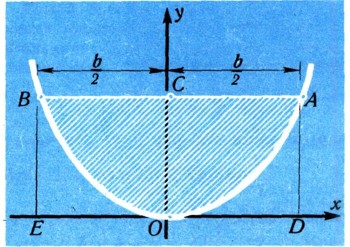 Рис. 15.
Но это значит, что 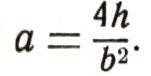 Итак, наш параболический сегмент ограничен снизу параболой, у которой в точке с абсциссой х ордината 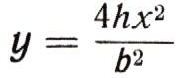 Мы легко можем теперь найти площадь криволинейного треугольника ОАD. По формулам (2) и (7) она равна: 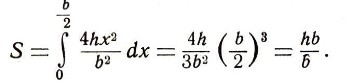 Площадь же прямоугольника ABED равна bh. Но площадь параболического сегмента получится, если из площади прямоугольника вычесть удвоенную площадь треугольника ОАО, т. е. она равна 2bh/3 . 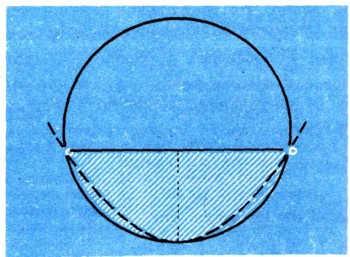 Рис. 16.
Круговой сегмент, имеющий небольшой центральный угол, можно приближенно заменить параболическим сегментом с той же хордой и той же стрелкой (рис. 16). Поэтому для площади кругового сегмента имеет место приближенная формула:  Например, если центральный угол равен 60°, то приближенная формула дает результат 0,0893...R2, а точная 0,0906...R2. Таким образом даже для такого сравнительно большого центрального угла, как 60°, приведенная формула дает точность до 1,5%. |
 |