Интеграл и производная |
Как сделать самую большую коробкуПусть перед нами квадратный кусок картона со стороной а. Из него надо сделать коробку без крышки. Вырежем по углам куска квадратики и согнем по линиям, отмеченным пунктиром (рис. 24). У нас получилась коробка; но много ли в нее можно положить? Это зависит от того, какие квадратики мы вырезали из этой коробки. Если они были очень маленькие, то коробка получится низкая (рис. 25) и в нее много не положишь. А если они будут слишком большие (рис. 26), то коробка получится слишком узкая и в нее тоже войдет довольно мало. Найдем, при какой стороне к вырезанного квадратика объем V(х) сделанной коробки будет наибольшим. Из рис. 24 видно, что V=x(a - 2х)2=4х3 - 4ах2 + а2х. График этой функции имеет вид, указанный на рис. 27. При этом х должен лежать между 0 и a/2, так как вырезать из куска картона со стороной а четыре квадрата со стороной, большей чем a/2, нельзя. Из рис. 27 видно, что в той точке, где значение объема наибольшее, касательная идет горизонтально, т. е. образует с осью х угол, равный нулю. Но это значит, что в этой точке производная равна нулю. Таким образом, чтобы найти значение Хmаx, при котором объем коробки будет самым большим, надо найти все значения х, при которых производная функции 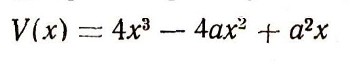
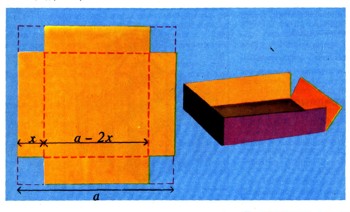 Рис. 24
 Рис. 25
 Рис. 26
обращается в нуль; среди них обязательно будет и искомое значение xmаx По формуле дифференцирования многочлена находим: 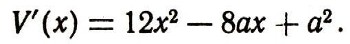
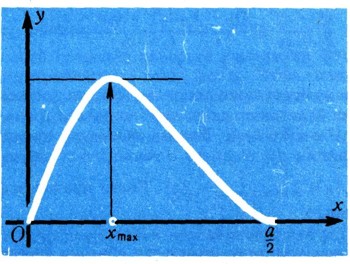 Рис. 27.
Приравниваем производную к нулю и находим два корня: х1=a/2, х2 =a/6. Разумеется, корень x1=a/2 нас не устраивает: если мы вырежем квадраты со стороной a/2, то от листа картона ничего не останется. Значит, наибольшее значение объема получится, если за xmax примем оставшееся значение a/6 т. е. вырежем квадраты со стороной x= a/6 . Объем коробки тогда будет равен 2a3/27. Сделать из данного куска картона коробку большего объема невозможно. |
 |