Множества и операции. Понятие множества. |
Взаимно однозначное соответствие между двумя множествамиПредположим, что мы имеем два конечных множества, например корзину яблок и корзину груш. Желая установить, чего у нас больше - яблок или груш, мы можем (и это будет самое простое решение вопроса) сосчитать число плодов в каждой корзине. Получим два числа, сравнение их и даст ответ на наш вопрос. Но если мы имеем два бесконечных множества, то определить аналогичным образом, какое из них является "более бесконечным", а какое - "менее", нельзя по той простой причине, что бесконечное множество нельзя "сосчитать". Во всяком случае, мы не знаем, как это сделать. Поэтому постараемся ответить на вопрос, чего у нас больше - яблок или груш, не сосчитывая их, т. е. не пользуясь понятием числа. Вот какой представляется для этого путь. Разложим наши яблоки, хотя бы на столе, и попробуем положить против каждого яблока пр груше. Возможны три случая (рис. 2).  Рис. 2.
Первый случай: против каждого яблока окажется груша, и при этом не только все яблоки, но и все груши окажутся разложенными. В этом случае, очевидно, у нас столько же яблок, сколько и груш. Второй случай: против каждого яблока окажется по груше, но при этом еще останется несколько "лишних" груш - в этом случае у нас больше груш, чем яблок. Наконец, возможен последний, третий случай: стараясь разложить все груши так, чтобы против каждого яблока лежала груша, мы не достигнем цели - нам не хватит груш. Тогда, очевидно, груш меньше, чем яблок. Как видите, мы смогли произвести количественную оценку двух множеств - корзины яблок и корзины груш, не сосчитывая точно, сколько имеется тех и других плодов, т. е. установить, каких плодов больше, или убедиться, что их имеется одинаковое количество. Эту оценку мы произвели, установив, как говорят, взаимно однозначное соответствие между одним множеством и другим или частью другого. Для лучшего уяснения, что такое взаимно однозначное соответствие между двумя множествами, приведем еще несколько примеров. Дается концерт. Чтобы на него пойти, надо купить билет. Перед нами два множества: множество людей, которые хотят пойти на этот концерт, - обозначим его через А - и множество билетов - обозначим его через В. Возможны разные случаи. Первый (не очень вероятный, но математически самый простой): все желающие пойти на концерт приобрели билеты, и все билеты при этом оказались проданными. Тогда каждому элементу множества А (т. е. каждому человеку, желающему пойти на концерт) соответствует определенный элемент множества В (купленный этим человеком билет). При этом каждый элемент множества В поставлен в соответствие одному-единственному элементу множества А (человеку, купившему этот билет). Установлено взаимно однозначное соответствие между множеством А и множеством В, или установлено взаимно однозначное отображение одного из этих множеств на другое. Однако может случиться, что каждый человек, желавший пойти на концерт, купил себе билет, но в кассе остались еще не распроданные билеты. Опять получается взаимно однозначное отображение множества А, но уже не на все множество В, а только на некоторую его часть - на ту часть, или, как говорят, на то подмножество множества В, которое состоит из всех проданных билетов. Может, наконец, случиться, что все билеты проданы, но не все желающие пойти на концерт смогли купить билеты. Тогда обозначим через А' множество тех людей, которые не только хотели пойти на концерт, но и получили на него билет. Множество А' оказалось взаимно однозначно отображенным на множество В. В математике можно найти многочисленные примеры взаимно однозначных соответствий. Например, каждой вершине треугольника или тетраэдра соответствует противоположная этой вершине сторона или грань. Таким образом, установлено взаимно однозначное соответствие между множеством всех вершин треугольника (тетраэдра) и множеством всех его сторон (граней). Множество всех сторон правильного многоугольника находится во взаимно однозначном соответствии с множеством всех перпендикуляров, которые опущены на эти стороны из центра правильного многоугольника. Множество всех боковых граней пирамиды находится во взаимно однозначном соответствии с множеством апофем этой пирамиды и т. д. Особенно существенным является тот факт, что взаимно однозначное соответствие возможно и между некоторыми бесконечными множествами. Приведем примеры. Обозначим через А множество всех точек данной окружности, а через В - множество всех прямых, являющихся касательными к этой окружности (рис. 3, I). Между множествами А и В установится взаимно однозначное соответствие, если мы каждой точке окружности поставим в соответствие касательную в этой точке. Таким образом, каждому элементу множества А соответствует единственный элемент множества В, и каждый элемент множества В (т. е. каждая касательная) при этом поставлен в соответствие единственному элементу множества А - точке прикосновения данной касательной. Второй пример. Возьмем две пересекающиеся прямые а1 и b1 (рис. 3, II). Обозначим через А множество всех точек прямой а1, а через В - множество, состоящее из прямой b1 и из всех прямых, ей параллельных. Каждому элементу b множества В (т. е. каждой прямой b, параллельной прямой b1 или совпадающей с ней) соответствует единственный элемент множества А - единственная точка прямой а1, в которой ее пересекает прямая b. 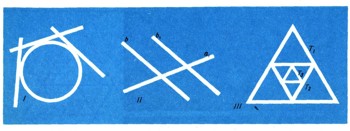 Рис. 3.
В качестве третьего примера возьмем уже рассмотренное нами множество равносторонних треугольников T1, T2, ... Tn, ... , В музее ... часовДа, есть и такой музей. Часов там много всяких: старинных и современных, механических и электрических, огромных и крошечных, с боем и без боя, с циферблатом и без циферблата. Первые механические часы были изобретены около середины X в. Очень долго часы имели лишь одну стрелку - часовую. Только в 1700 г. появилась и минутная стрелка, а еще через 60 лет - секундная. 400 лет часы приводятся в действие пружиной. Но эра пружины на исходе. Современные наручные электронно-механические часы совсем и заводить не надо. В числе тикающих и безмолвствующих обитателей музея была пара действующих часов с боем, одинаковым по тембру. Однажды они ударили подряд, как я насчитал, 19 раз. (Это произошло потому, что начало боя на первых часах опаздывало по отношению ко вторым часам на 2 секунды. Кроме того, первые часы, оказывается, ударяли через каждые 3 секунды, а вторые - через 4 секунды. Который был час? Ответы и решенияРешение. Пусть число рыб в озере, годных для улова данной сетью, равно х. Товда отношение числа меченых рыб к числу всех рыб равно 38/x. Во второй раз рыбовод выловил 53 рыбы, из них две меченые. Следовательно, отношение числа меченых рыб к числу выловленных равно 2/53 Будем предполагать, что меченые рыбы равномерно распределились среди всех рыб в водоеме, тогда оба отношения одинаковы: 38/x=2/53 , откуда х=1007. Значит, в озере имеется примерно тысяча рыб, годных для улова данной сетью. Ответ. 1000000000=109=(2*5)9=29*59 = 51,2*1953126. 1 000 000 000 000 000 000 = 1018 = 218 * 518= 262 144 * 3 814 697 265 625. каждый из которых, кроме первого, вписан в предыдущий (рис. 3, III). Множество всех этих треугольников обозначим через X. Каждый треугольник получил определенное натуральное число п в качестве своего номера. Номером треугольника Тn является натуральное число п. Этим, очевидно, установлено взаимно однозначное соответствие между множеством X наших треугольников и множеством всех натуральных чисел. |
 |