Множества и операции. Понятие множества. |
Множество всех рациональных чисел счетноВ поисках несчетного множества обратимся к множеству всех рациональных чисел (читатель, конечно, помнит, что рациональными числами называются все целые и все дробные числа). Посмотрим, можно ли занумеровать все рациональные числа с помощью натуральных. Для простоты рассмотрим сначала все положительные рациональные числа и попробуем их как-нибудь занумеровать. Сразу же сталкиваемся с трудностью: среди положительных рациональных чисел заведомо нет наименьшего числа, каким является единица среди натуральных чисел; ведь, каково бы ни было положительное рациональное число r, число 1/2r также является положительным рациональным числом, и оно меньше, чем r. Предположим, мы обойдем эту трудность, начав счет с какого-нибудь рационального числа r1, которое согласимся считать первым. Но тогда на следующем этапе возникает такая трудность: какое рациональное число считать вторым, т. е. непосредственно следующим в порядке нашего счета за числом r1 Дело в том, что, какое бы рациональное число r2>r1 мы ни взяли, имеются рациональные числа большие, чем r1, и меньшие, чем r2, и таких бесконечное множество, например числа: 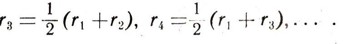 Таким образом, среди всех рациональных чисел, больших чем выбранное нами число r1, нет наименьшего. Какое же объявить первым из следующих за r1? Но возникшая трудность кажущаяся. Она показывает только, что невозможно занумеровать рациональные числа с помощью натуральных чисел таким образом, чтобы при этой нумерации возрастающим номерам соответствовали возрастающие числа. Придется попытаться занумеровать рациональные числа как-нибудь иначе, не стремясь к тому, чтобы число r1, первое после r1 в порядке нашего счета, было и первым по величине, т. е. наименьшим из всех следующих за r1. А тогда нужная нам нумерация находится очень легко. В самом деле, каждое положительное рациональное число однозначно записывается в виде несократимой дроби p/q (целое число n будем при этом записывать в виде дроби n/1 и также считать ее несократимой). Назовем высотой дроби - натуральное число q + p. Под высотой рационального числа будем понимать высоту той единственной несократимой дроби, которая является записью данного числа. Посмотрим, сколько приходится рациональных чисел на каждую данную высоту. Высоту 1 не имеет ни одно положительное рациональное число (потому что, записывая рациональное число в виде несократимой дроби - , видим, что ее высота равна натуральному числу p + q, а так как р>=1, q>=1 то p + q>=2). Высоту 2 имеет, очевидно, единственное рациональное число 1/1=1. Высоту 3 имеют дроби 1/2и 2/1 т. е. рациональные числа 1/2 и 2. Высоту 4 имеют дроби 1/3,2/2, 3/1. Среди них оставляем лишь несократимые 1/3 и 3/1 . Итак, высоту 4 имеют рациональные числа 1/3 и 3. Высоту 5 имеют дроби 1/4, 2/3, 3/2, 4/1, среди которых нет сократимых, так что на высоту 5 приходится 4 числа. Высоту 6 имеют дроби 1/5, 2/4, 3/3, 4/2, 5/1, среди которых несократимы лишь первая и последняя; следовательно, высоту 6 имеют числа 1/5 и 5. Продолжая рассуждать таким образом дальше, мы прежде всего убеждаемся в том, что, каково бы ни было натуральное число h>1, есть лишь конечное число рациональных чисел с этой высотой. В самом деле, дроби с высотой h - это, очевидно, 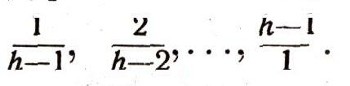 Их конечное число: h -1. Среди этих дробей некоторые могут оказаться сократимыми, а остальные дадут рациональные числа с высотой h. Теперь уже очень легко занумеровать все положительные рациональные числа: мы начинаем с наименьшей высоты 2 и идем дальше, все время увеличивая на единицу высоту и сосчитывая то (всегда конечное) число рациональных чисел, которое приходится на данную высоту. Таким образом, число 1=r получает номер 1. Далее идут два числа: r2=1/2 и r3 = 2 высоты 3, потом два числа: r4=1/3 и r5 = 3 высоты 4, потом четыре числа: r6 = 1/4, r7 =2/3, r8 =2/3, r9 = 4 высоты 5, два числа: r10 =1/5, r11 = 5 высоты 6 и т. д. Получаем таблицу (через nh обозначено число рациональных чисел высоты h):
Так как каждое рациональное число имеет своей высотой некоторое натуральное число h, оно найдет свое место в строке, соответствующей этой высоте, и получит определенный номер, не больший чем число n2 + n3 + ... + nh-1 + hh Итак, множество всех положительных рациональных чисел есть счетное множество. |
 |