Множества и операции. Понятие множества.

Множество всех действительных чисел несчетно

И тем не менее несчетные множества существуют. Оказывается, множество всех действительных чисел несчетно. Этот замечательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем теории множеств. Воспроизводим доказательство Кантора. Доказываем, что несчетным является уже множество всех действительных чисел интервала (0; 1).

Под интервалом (а; 6) числовой прямой понимается множество всех действительных чисел х, удовлетворяющих неравенству а<x<b. Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь одна такая запись, за исключением действительных чисел, выражаемых конечными десятичными дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби: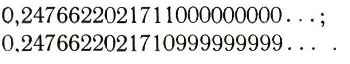

Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая - одни девятки. Если мы согласимся не употреблять записей, в которых начиная с какого-нибудь места идут одни девятки, то каждое действительное число будет иметь лишь единственную запись в виде бесконечной десятичной дроби. Докажем теперь теорему о несчетности множества действительных чисел от противного: предположим, что множество действительных чисел (мы говорим все время о числах X интервала (0; 1) счетно, т. е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0; 1) может быть записана в виде последовательности: х₁, x₂, ... Запишем разложение числа Хп в бесконечную десятичную дробь: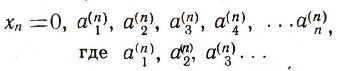

суть, последовательные десятичные знаки числа х_nпричем, согласно заключенному нами условию, не может случиться, что все десятичные знаки начиная с некоторого суть девятки. Итак, все действительные числа х (интервала (0; 1) предполагаются записанными в виде: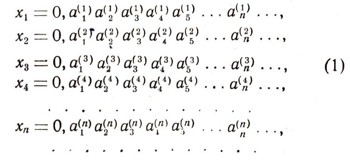

Приведем наше предположение к противоречию, найдя действительное число с, заключенное между 0 и 1 и заведомо не входящее в табл. (1). Для этого рассмотрим цифры, стоящие по диагонали в табл. (1), а именно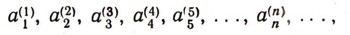

и выберем для каждого п натуральное число b_n, не превосходящее число 8 и отличное от числа а⁽ⁿ⁾ (например, при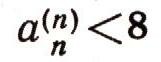

полагаем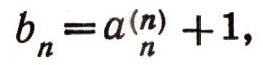

а при а⁽ⁿ⁾=8 полагаем b_n=7). Рассмотрим бесконечную десятичную дробь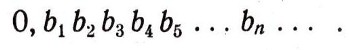

Она не содержит ни одной девятки и выражает число с, заключенное между 0 и 1, заведомо отличное от всех чисел х₁, х₂, х₃, ..., х_п, ... В самом деле, если бы было: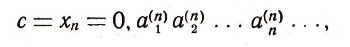

то на n-м месте в разложении числа с мы должны были бы иметь цифру а⁽ⁿ⁾ тогда как в действительности имеем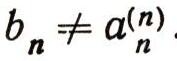

Теорема доказана.