Алгебра множеств и алгебра логики. |
Алгебра чиселВ арифметике и алгебре рассматривают числа разной природы - целые числа, рациональные числа (дроби) и другие. Во всех случаях с каждыми двумя числами а и b сопоставляются еще два числа: а + b и ab, называемые суммой и произведением чисел а и b. Определение суммы и произведения двух чисел различно для чисел разной природы. Так, если а есть целое положительное число, то его можно представлять себе как число предметов в некотором наборе. При этом сумма а + b означает число предметов, которые мы получим, если объединим первый набор, содержащий а предметов, и второй набор, содержащий b предметов (рис. 1). Если же объединим b наборов, каждый из которых содержит по а предметов, то всего мы получим ab предметов (рис. 2). Более сложно определяются сумма и произведение дробей, например так: 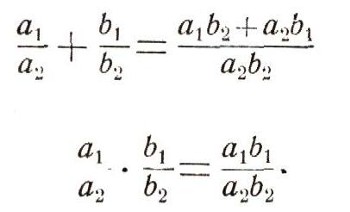
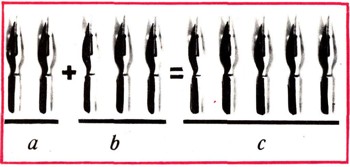 Рис.1. а+b=с
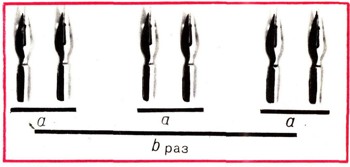 Рис.2. a*b = c
(Здесь числа а1, а2, b1, b2 целые.) Иные правила относятся к сложению и умножению отрицательных чисел, среди этих правил есть, скажем, такое: 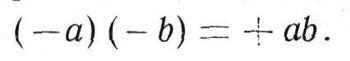 Но независимо от природы рассматриваемых чисел и от определения суммы и произведения чисел общие законы действия над числами остаются одни и те же. Вот эти законы: 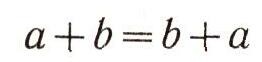 (коммутативный, или переместителъный, закон для сложения); 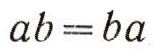 (коммутативный, или переместительный, закон для умножения); 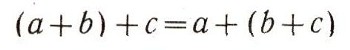 (ассоциативный, или сочетательный, закон для сложения) ; 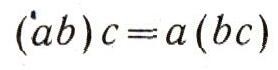 (ассоциативный, или сочетательный, закон для умножения); 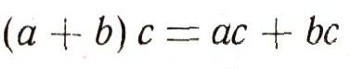 (дистрибутивный, или распределительный, закон для умножения (относительно сложения)). При этом сразу бросается в глаза, что правила, относящиеся к сложению чисел, очень похожи на правила умножения. Например: 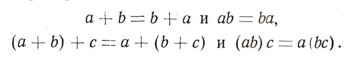 Это сходство между действиями сложения и умножения находит отражение и в существовании двух замечательных чисел 0 и 1, таких, что прибавление одного из них и умножение на второе не меняют ни одного числа: 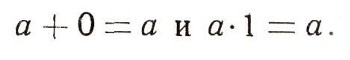 Следует, впрочем, заметить, что сходство между действиями сложения и умножения не простирается особенно далеко. Так, например, число 0 играет особую роль не только по отношению к сложению, но и по отношению к умножению: эта особая роль числа 0 определяется замечательным равенством а. 0 = 0. (Из этого равенства, в частности, вытекает, что делить на 0 число а = 0 нельзя.) В противоположность этому числу 1 по отношению к операции сложения не играет никакой особой роли: равенство, которое получается из равенства а * 0 = 0 заменой числа 0 на число 1 и операции умножения - операцией сложения: 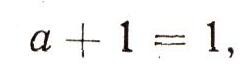 почти никогда не будет верным. (Это равенство справедливо лишь при а = 0.) Так же и дистрибутивный закон 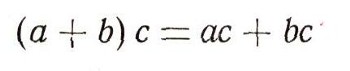 подчеркивает различие между действиями сложеню и умножения. Если заменить в записи этого закон; сложение умножением и наоборот, то получим курь езное "равенство": 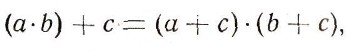 как правило, не выполняющееся: так, 1*2 + 3 = 5, а (1+3) * (2 + 3) = 20. (Нетрудно видеть, что равенство (a-b) + c = (a + c)*(b + c) справедливо лишь при с = 0 и при а + b + с = 1.) В математике, однако, операции сложения и умножения определяются не только для чисел. При этом иногда удается прийти к "алгебре", в которой сходство между операциями сложения и умножения оказывается большим, чем в обычной "числовой" алгебре. В качестве примера можно указать "алгебру множеств". |
 |