Алгебра множеств и алгебра логики. |
"Нуль" и "единица"Выясним, существует ли в "алгебре множеств" такой элемент 0 ("нуль"), что прибавление его к любому множеству А не меняет этого множества. Ясно, что последнее возможно только в том случае, если "множество 0" - совсем не содержит элементов, является "пустым". Но в последнем случае не хочется даже говорить о "множестве": какое же это множество, состоящее из отдельных элементов, если этих элементов вовсе нет? В учении о множествах, однако, целесообразнее причислять пустое множество, вовсе не содержащее элементов, к числу рассматриваемых множеств. Ведь в противном случае мы зачастую не сможем говорить о множестве, не выяснив предварительно, существует оно или нет. Так, прежде чем сказать: "Множество отличников из IX класса "А" школы № 13 Ленинграда", нам придется пойти в школу и справиться об успеваемости учеников этого класса. Гораздо удобнее спокойно говорить об этом множестве, оговорив только, что оно может быть и пустым, т. е. не содержать ни одного элемента. В ряде случаев мы можем заранее сказать, что то или иное множество не является пустым; так, не пустое, разумеется, множество самых высоких учеников класса (это множество может иногда содержать и больше одного ученика). В иных случаях мы сразу скажем, что множество, о котором идет речь, пустое. Так, конечно, пустым является множество обучающихся в вашем классе живых слонов или множество учеников, рост которых превышает 2,5 м. Однако в большинстве случаев лишь более тщательный анализ позволяет указать, является то или иное множество пустым или нет. Так, например, множество Семенов или множество левшей из вашего класса может оказаться пустым или не пустым. Пустое множество в дальнейшем всегда будем обозначать знаком О. Таким образом, для каждого множества А будем иметь (рис. 14): 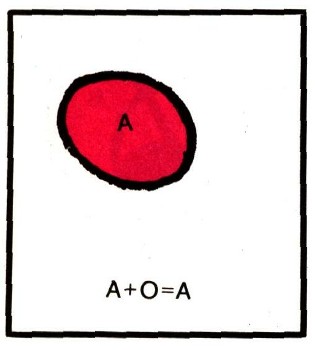 Рис. 14.
А + О = А. Подобно известному правилу а * 0 = 0 алгебры чисел, для любого множества А также имеем: А * 0=0. В самом деле, множество А * О, по определению, состоит из всех элементов, принадлежащих и множеству А и множеству О. Но множество О вовсе не содержит элементов; поэтому не может содержать элементов также и множество А * О (или АО). Теперь зададимся вопросом о "множестве 1", обладающем тем свойством, что произведение его на любое множество А дает А. Последнее означает, что пересечение или общая часть "множества 1" и множества А для любого множества А совпадает с самим этим множеством. Но это возможно, разумеется, лишь в том случае, если "множество 1" содержит все вообще существующие элементы. Так, если мы рассматриваем всевозможные множества учеников из нашего класса, то роль единицы будет играть множество всех обучающихся в классе учеников. Нетрудно понять, что, скажем, произведение этого множества и множества А отличников будет состоять из всех отличников (т. е. совпадать с А); произведение этого множества и множества В сидящих в первом ряду учеников будет состоять из всех учеников, сидящих в первом ряду (т. е. будет совпадать с множеством В). Множество, состоящее из всех элементов всех рассматриваемых множеств, называется полным, универсальным или единичным; мы будем обозначать его знаком I. Таким образом, для любого множества А: А * I = А. Универсальное множество I графически изображается всем квадратом, внутри которого мы рисуем фигуры, изображающие различные множества (рис. 15).  Рис. 15.
|
 |