Алгебра множеств и алгебра логики. |
Отрицание. Отношение следствияПродолжим построение алгебры высказываний. При изучении множеств мы наряду с операциями сложения и умножения множеств рассматривали также операцию "взятия дополнения", сопоставляющую с каждым множеством А его дополнение А. Этой операции отвечает чрезвычайно важная операция алгебры высказываний, сопоставляющая с каждым высказыванием а новое высказывание а, называемое отрицанием а. Грамматически отрицание а получается из высказывания а при помощи частицы "не"; например, отрицанием высказывания "он отличник" является высказывание "он не отличник" (рис. 29). Множество истинности высказывания а является дополнением множества истинности высказывания а; это утверждение можно даже считать определением отрицания.  Рис. 28.
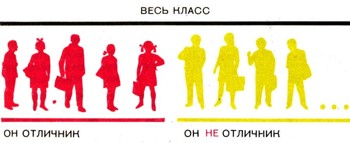 Рис. 29
Алгебраические свойства дополнения множеств сразу приводят к следующим утверждениям, связанным с отрицанием высказываний: 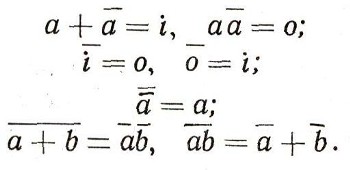 Введем, наконец, еще одно отношение, связывающее два высказывания. А именно, пусть множество истинности А высказывания а уже множества истинности В высказывания b; другими словами, пусть А целиком содержится в В (т. е. А [ В или В ] А). В таком случае мы будем говорить, что высказывание а влечет высказывание b или что b следует из а (или что b является следствием а). Например, если множество отличников класса состоит из школьников Гриши, Илюши и Пети, то высказывание "Он отличник" влечет за собой истинность высказывания "Он мальчик" (или высказывание "Он мальчик" следует из высказывания "Он отличник"; см. рис. 30). Отношение следствия имеет естественно подразумеваемый словом "следствие" смысл: если b следует из а и мы знаем, что высказывание а истинно, то, наверное, истинно и высказывание b.  Рис. 30
Так, в разобранном выше примере истинность утверждения "Он отличник" означает, что речь идет об одном из трех школьников - Грише, Илюше или Пете; но тогда истинно и высказывание "Он мальчик". Отношение следствия играет в алгебре высказываний такую же роль, какую в алгебре множеств играет отношение с, указывающее, что одно множество содержится в другом; иногда его обозначают тем же значком с . Однако чаще отношение "а влечет b" (или, что то же самое, "6 следует из а") записывается так: а=>Ь. Запись а=>b читается как "b следует из а" или, короче, как утверждение "если а, то b". При этом часто говорят, что а является достаточным условием для b: если мы знаем, что высказывание а является истинным, то этого достаточно, чтобы не сомневаться и в истинности высказывания b. Так, если в условиях проиллюстрированного (рис. 30) примера мы знаем, что "он (какой-то учащийся рассматриваемого класса) отличник", то этого достаточно, чтобы утверждать, что "он мальчик". Напротив, про высказывание b, такое, что а => b, говорят, что оно является необходимым условием для а. Так, в рассмотренном выше примере условие "Он мальчик" является, конечно, необходимым условием истинности высказывания "Он отличник", ибо ни одна девочка в классе отличником не является; однако это условие не является достаточным, поскольку наугад выбранный мальчик может и не оказаться отличником. (Напротив, условие "Он отличник" достаточно, но не необходимо для истинности высказывания "Он мальчик" - учащийся может и не быть отличником, но при этом оказаться мальчиком.) В соответствии с этой терминологией об эквивалентных высказываниях а и b (высказываниях, для которых а<=>b) часто говорят, что каждое из них является необходимым и достаточным условием второго. Так, например, если в некоторой группе школьников все девочки являются отличницами, а все мальчики не отличники, то для этой группы ребят условие а ("Она девочка") является необходимым и достаточным для истинности высказывания b ("Он (школьник) - отличник"): здесь и а => b и b=>а. Из известных свойств алгебры множеств, связанных соотношением => , следует, что: 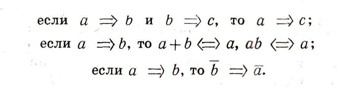
|
 |