Группы |
Группы симметрииПосмотрите на геометрические фигуры, изображенные на рис. 7. Фигуру А на этом рисунке никак нельзя назвать симметричной. Фигуры В и С уже обладают некоторой симметрией. Более симметрична фигура D, и, конечно, самой симметричной из всех начерченных фигур является фигура Е (квадрат). 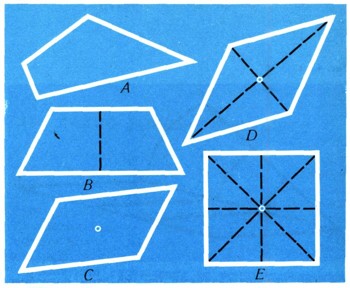 Рис. 7.
Однако это только слова - симметричность не длина и не площадь, а потому понятия "больше" и "меньше" для оценки симметричности пока точного смысла не имеют. Как же можно оценить большую или меньшую симметричность фигуры? Для этого надо рассмотреть множество всех движений плоскости, которые переводят рассматриваемую фигуру самое в себя. Для фигуры А на рис. 7 единственным таким движением является тождественное преобразование. Для фигур В и С кроме тождественного преобразования есть еще по одному движению, переводящему их в себя, именно: для равнобочной трапеции - осевая симметрия (относительно прямой, соединяющей середины оснований), для параллелограмма - центральная симметрия. Для ромба D есть уже 4 движения, совмещающих его с самим собой: тождественное преобразование, две осевые симметрии относительно диагоналей и центральная симметрия. Наконец, для квадрата таких преобразований 8 (4 осевые симметрии относительно средних линий и диагоналей и 4 вращения на углы 0°, 90°, 180° и 270°). Ясно, что совокупность всех движений, переводящих заданную геометрическую фигуру самое в себя, образует группу. В самом деле, если преобразования а и бета переводят фигуру F в себя, то и их произведение а * бета преобразует ее в себя. Не изменит ее, конечно, и тождественное преобразование. То же самое верно и для обратного преобразования. Группу всех движений, переводящих фигуру F самое в себя, называют группой симметрии этой фигуры. Чем шире группа симметрии данной фигуры, тем более симметричной она является. Именно поэтому квадрат является наиболее симметричной из всех фигур, изображенных на рис. 7. Интересные примеры симметричных фигур, обладающих самыми разными типами симметрии, дают узоры. Если фигура переходит сама в себя при всех поворотах на углы вида 360°*k/n, где k - целое, а п фиксировано, то говорят, что она обладает симметрией порядка п (см. стр. 299). Такой симметрией обладает, например, правильный n-угольник. Бывают фигуры, у которых группа симметрии бесконечна. Примерами могут служить окружность, кольцо, а также фигуры, эти фигуры надо представить себе простирающимися в бесконечность). Разумеется, о группе симметрии можно говорить не только для плоских, но и для пространственных фигур. При этом обычно рассматривают только движения пространства, не являющиеся симметриями относительно плоскостей (их нельзя осуществить в пространстве движениями пространственных тел как твердого целого). Так, можно говорить о группе симметрии правильного тетраэдра, куба, икосаэдра, правильной я-угольной призмы и т. д. Предоставляем читателю убедиться, что группа симметрии куба состоит из 24 элементов, а правильной n-угольной призмы - из 2п элементов. |
 |