Группы

Группы алгебраических преобразований

Преобразования можно производить не только над геометрическими фигурами, но и над алгебраическими выражениями. Речь идет здесь, конечно, не о тождественных преобразованиях (раскрытии скобок, приведении подобных членов и т. д.). Нет, мы будем рассматривать такие преобразования, как изменение знаков переменных, перестановки переменных и т. д. Например, многочлен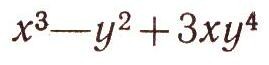

при изменении знаков переменных х и у превращается в многочлен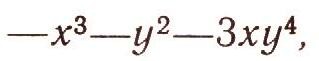

а при перестановке х и у - в многочлен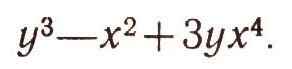

Изучение преобразований алгебраических выражений представляет собой с точки зрения эрлангенской программы ф. Клейна своеобразную геометрию. В этой геометрии "фигурами" являются алгебраические выражения (многочлены, дроби и т. д.), а группа преобразований состоит в одних случаях из всевозможных перестановок переменных, в других - из циклических перестановок переменных (при которых каждое переменное заменяется следующим, а последнее - первым), в третьих - из всевозможных замен знаков переменных (рис. 9) и т. д.

Задачей такой геометрии, как и обычной геометрии, является нахождение таких свойств "фигур" (т. е. алгебраических выражений), которые сохраняются при всех преобразованиях данной группы. В частности, весьма интересно нахождение и изучение "симметричных фигур" для данной группы, т. е. алгебраических выражений, которые не изменяются при преобразованиях данной группы. Например, если рассматривать группу всех перемен знаков, то "симметричными фигурами" будут четные выражения, т. е. такие, у которых показатели всех степеней переменных четны (например, х² + y⁴, х² + 5 - x⁸y⁶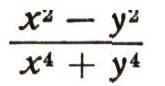

и т. д.). Для группы всех перестановок переменных "симметричными фигурами" будут такие выражения, которые не меняются ни при каких перестановках переменных. Они называются симметрическими функциями. Например, симметрическими многочленами от двух переменных х, у являются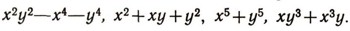

В такой геометрии есть и свои теоремы. Например, можно доказать, что любой симметрический многочлен от х и у выражается через два простейших многочлена х+у и ху. Скажем,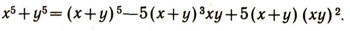

Эту теорему можно применять при решении систем уравнений. Если оба уравнения системы двух уравнений с двумя неизвестными симметричны относительно х я у, то бывает полезно ввести новые неизвестные: и = х + у, v = xy. Как правило, после этого заданная система уравнений упрощается. Например, система уравнений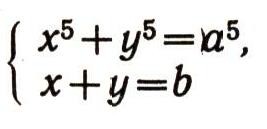

при такой замене сводится к системе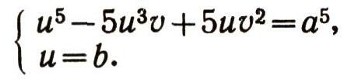

Из этой системы легко найти u и v, а потом х b у. Любопытно, что теория групп первоначально и возникла при рассмотрении групп алгебраических преобразовании. Чтобы узнать, решается ли данное алгебраическое уравнение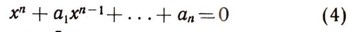

в радикалах, алгебраисты стали рассматривать значения, которые принимают многочлены от п переменных, если в них вместо х₁, х₂, ..., х_n подставить корни а₁, а₂, ... аⁿ уравнения (4). Оказалось, что вопрос о разрешимости уравнений в радикалах тесно связан с поведением этих значений многочленов при различных перестановках корней между собой.

Эти исследования привели к созданию новой, очень глубокой и важной ветви алгебры - применению теории групп к исследованию уравнений. Основоположные результаты этой теории были получены в 1830-1832 гг. французским математиком Э. Га-луа. В его честь весь этот раздел алгебры носит сейчас название теории Галуа.