Выдающиеся математики

Омар Хайям

Омар Хайям, один из крупнейших математиков средневекового Востока, поэт и философ, родился в 1048 г. (предположительно), умер в 1131 г. Он был уроженцем Нишапура, главного города Хорасана, страны, лежавшей к юго-востоку и востоку от Каспийского моря.

В молодые годы Хайяму пришлось много скитаться. Он жил и работал в Самарканде и Бухаре, а в 1076 г. был поставлен во главе обсерватории, организованной в столичном городе Исфахане. Здесь ученый разработал проект нового весьма точного календаря, который не смог, однако, найти применения. Вскоре один за другим умерли покровительствовавшие Хайяму первый министр Низам-аль-Мульк и султан Мелик-шах, и обсерватория была закрыта. Мусульманское духовенство ненавидело вольнодумца Хайяма. При преемниках Мелик-шаха влияние духовенства усилилось, и Хайям впал в немилость.

Математические сочинения Хайяма относятся к алгебре, арифметике и геометрии. Они написаны на арабском языке, которым, как правило, пользовались ученые в странах Азии и Африки, покоренных арабами.

Главный труд Хайяма называется "Трактат о доказательствах задач алгебры и ал-мукабалы". Уравнения в то время приводили для решения к нормальному виду, располагая в обеих частях уравнения члены с положительными коэффициентами. Так, например, различали три вида квадратных уравнений: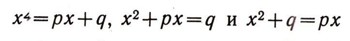

и для каждого формулировали свой особый прием решения. Уравнение x² + px + q=0 вовсе не рассматривалось, так как при р>=0, q>=0 у него не может быть положительных решений, а только они одни в то время и принимались во внимание. Операция переноса вычитаемых членов данного уравнения в другую часть, где они оказываются уже прибавляемыми, называлась ал-джебр ("восполнение"). Операция приведения подобных членов в обеих частях уравнения называлась ал-мукабала ("противопоставление"). От слова "ал-джебр" произошло наше слово "алгебра", и уже у Хайяма говорится об "алгебраистах".

Трактат Хайяма посвящен в основном кубическим уравнениям. Первые задачи, приводящие к кубическим уравнениям с целыми корнями, которые легко найти с помощью простого подбора, появились еще в древнем Вавилоне. Древние греки нашли геометрический прием построения положительных корней кубических уравнений. Прежде всего они применили его к задаче об удвоении куба, т. е. отыскании ребра х такого куба х³, который был бы вдвое больше данного куба а³. Величину х, т. е. корень уравнения х³ = 2а³, они строили как абсциссу точки пересечения двух парабол с уравнениями 2ах = у² и ау = х², отличной от начала координат. Затем Архимед свел к уравнению вида х³ + r = рх² задачу о делении шара плоскостью на два сегмента, объемы которых находятся в данном отношении. Он построил корень этого уравнения как абсциссу точки пересечения некоторых параболы и гиперболы и произвел тщательный анализ задачи.

Проблема Архимеда заинтересовала математиков арабских стран еще в середине IX в. Вскоре здесь занялись и другими вопросами геометрии, приводящими к уравнениям третьей степени. Такие уравнения имеют важное значение и для астрономии, а именно для вычисления необходимых астрономам тригонометрических таблиц. Дело в том, что вычисление синуса 1° можно привести к решению уравнения вида x³ + r = qx. Ученые создали различные приемы приближенного вычисления корней уравнений третьей степени. Наряду с этим возникла потребность в более общей теории.

Наиболее полную для своего времени теорию разработал Хайям, широко применив геометрический метод древних греков. Он рассмотрел все нормальные виды кубических уравнений, которые могут иметь положительные корни. Всего таких видов оказалось 14: одно двучленное, шесть с тремя членами и семь четырехчленных. Для каждого вида Хайям приводит соответствующее ему построение. Так, корень трехчленного уравнения x³ + qx-,r выражается абсциссой той точки пересечения окружности х² + у²= rх/q и параболы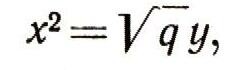

которая отлична от начала координат. Анализируя построение, Хайям выясняет, при каких условиях уравнение даннoго вида имеет один или два положительных корня. Например, уравнение х³+qх=r при любых значениях коэффициентов имеет один, и только один, положительный корень. Иногда Хайям указывает границы, в которых лежит корень уравнения того или иного вида. На примерах Хайям показывает, как общая теория применяется к исследованию уравнений с данными числовыми коэффициентами.

Все же в исследовании Хайяма есть пробелы. Так, он не заметил, что уравнение вида х³ + qx =^:рх² + r может иметь в некоторых случаях три положительных корня. Обнаружить это только с помощью чертежа трудно.

Как и другие математики средневекового Востока, Хайям пытался найти формулу для выражения корня кубического уравнения с помощью радикалов, подобно формулам корней квадратного уравнения. Достичь успеха ему не удалось. Только в начале XVI в. итальянские математики открыли выражение корня кубического уравнения с помощью кубических и квадратных радикалов. Но уже Хайям пришел к убеждению, что сделать это с помощью квадратных радикалов в общем случае невозможно. Геометрическая теория кубических уравнений получила дальнейшее развитие как на Востоке, так и в Европе, в частности у Р. Декарта. В XVI-XVII вв. геометрические приемы исследования начинают быстро вытесняться алгебраическими, более совершенными и удобными. Все же до сих пор иногда пользуются геометрическим построением корней уравнений (не только кубических), чтобы примерно определить их значение или получить общее представление о числе положительных и отрицательных корней и т. п.

В алгебраическом трактате Хайям упоминает свой труд по арифметике, в котором он изложил прием извлечения корней любой целой положительной степени из чисел. (Ранее были известны способы извлечения квадратного и кубического корней.) Этот его труд до сих пор не обнаружен. Вероятно, Хайям вывел в нем так называемую формулу бинома Ньютона для целого положительного показателя. Впервые она встречается у другого выдающегося среднеазиатского математика - Насирэддина Туси в учебнику, написанном в 1265 г.

Подобно грекам, математики стран Арабского Востока не имели никаких алгебраических обозначений и все уравнения, преобразования и т. д. записывали словами. Это чрезвычайно удлиняло и затрудняло как исследование, так и изложение. Нашему современнику, приученному к экономной и изящной символической записи, трудно читать старинные трактаты по алгебре.

Хайям написал также комментарии к "Началам" Евклида, в которых высказал ряд интересных мыслей по теории параллельных линий, оказавших влияние на дальнейшее развитие геометрии.