Выдающиеся математики |
Жозеф Луи ЛагранжВ 1736 г. в итальянском городе Турине, входившем тогда в состав Сардинского королевства, в семье военного казначея Лагранжа родился одиннадцатый ребенок, получивший при крещении имя Жозеф Луи. Когда мальчик вырос, его отдали в артиллерийскую школу, которая готовила военных специалистов, владеющих теорией артиллерийской стрельбы. Для успешного овладения этой теорией требовалась хорошая математическая подготовка, поэтому математика занимала видное место в процессе обучения. Выявившиеся выдающиеся математические способности Жозефа Луи позволили ему не только успешно окончить артиллерийскую школу Турина, но уже в возрасте 19 лет занять в ней место профессора математики. Вскоре вокруг молодого талантливого ученого образовался кружок интересующейся наукой молодежи, который впоследствии перерос в Туринскую академию. Первый том ее трудов увидел свет в 1759 г. Значительная часть работ, печатавшихся в этом издании, принадлежала самому Лагранжу. Среди различных вопросов, занимавших его в то время, выделялся один, разработке которого он уделял особенное внимание. Исследование этого вопроса привело к замечательным результатам, лежащим в основе вариационного исчисления.  Чтобы дать читателю представление о том, что изучается в этом разделе математики, рассмотрим одну из задач вариационного исчисления, история которой уходит в глубокую древность. Речь пойдет о зависимости между длиной замкнутой кривой на плоскости и площадью, ею ограниченной. Верно ли предположение, что большая по длине кривая охватывает фигуру большей площади? Так думали древние путешественники, измеряя величину открытого ими острова длиной его береговой линии. Многие люди, пишет древнегреческий историк Полибий, судят о величине города по длине крепостных стен. Им кажется невероятным, что Спарта, со стеной длиной в 48 стадий, вдвое больше Мегаполиса, имеющего стену длиной в 50 стадий. Из рис. 1 видно, что площадь квадрата ABCD больше площади заштрихованной фигуры, хотя длина границы последней превышает сумму длин сторон квадрата. Значит, высказанное выше предположение неверно. Естественным образом возникает задача - среди всех замкнутых кривых данной длины на плоскости найти ту, которая ограничивает наибольшую площадь. Античными геометрами было доказано, что такой кривой является окружность. 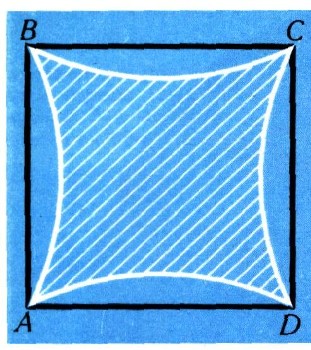 Рис. 1
Некоторым усложнением предыдущей задачи является следующая. Пусть на горизонтальной плоскости в двух точках А и В закреплена нить фиксированной длины (большей, чем расстояние между этими точками, см. рис. 2). Будем произвольно менять ее положение, соблюдая следующие условия: 1) ни одна точка нити не должна находиться ниже прямой АВ (рис. 3); 2) нить не имеет точек самопересечения. Пусть нить приняла положение, отмеченное на рис. 3 цифрой I. Рассмотрим фигуру, заключенную между отрезком АВ и нитью в этом положении (на рис. 3 заштрихована). Обозначим ее площадь через S. Ясно, что площадь будет изменяться в зависимости от положения нити. Теперь сформулируем задачу: найти такое возможное положение нашей нити (другими словами, такую гладкую кривую фиксированной длины, проходящую через точки А и В), чтобы значение S было наибольшим. Нахождение соответствующих выражений, зависящих от кривых на плоскости, и нахождение тех кривых, для которых эти выражения принимают наибольшие и наименьшие значения, - эти вопросы решаются средствами вариационного исчисления. (К сожалению, дать сколько-нибудь полное представление об этой науке и даже аккуратно сформулировать задачу, приведенную выше, здесь невозможно.)  Рис. 2
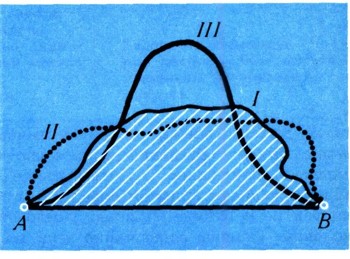 Рис. 3
Такого рода "принципы экономии" характерны для описания различных процессов, изучаемых физикой и механикой. Так, свет, распространяющийся из одной точки в другую, следует по тому пути, для прохождения которого ему требуется наименьшее время (принцип, установленный П. Ферма). Подобными задачами занимались многие видные математики, достаточно назвать имена Якоба и Иоганна Вернулли, Б. Тейлора. Однако лишь в трудах знаменитого Леонарда Эйлера задачи такого рода были объединены в рамках единого исчисления, которому сам Эйлер дал название вариационного. О своих результатах по вариационному исчислению Лагранж написал в 1755 г. Эйлеру, который был настолько восхищен гением молодого ученого и значением полученных им результатов, что решил не опубликовывать свои собственные работы в этом направлении до появления в печати статьи Лагран-жа. Статья появилась во II томе записок Туринской академии и принесла ее автору славу одного из создателей (наряду с Эйлером) вариационного исчисления. Имя Лагранжа приобретает европейскую известность, по представлению Эйлера его избирают членом Берлинской академии. А уже в 1766 г. по рекомендации того же Эйлера, покидавшего Берлин с тем, чтобы уже навсегда переселиться в Россию, он получает приглашение прусского короля Фридриха II занять кресло президента Берлинской академии. Еще в Турине Лагранж начал заниматься приложениями вариационного исчисления к задачам механики. Постепенно у него возник грандиозный замысел: используя мощь современного ему математического анализа, переработав достижения в области механики крупнейших ученых XVIII в., наконец, взяв в качестве объединяющей основы вариационное исчисление, совершенно перестроить начиная с фундамента все здание механики. И если в классическом изложении Ньютона, выполненном за 100 лет до этого, механика выступала как раздел натуральной философии, т. е. науки о природе, то у Лагранжа она должна была стать отраслью математического анализа. Его план был реализован в главном сочинении его жизни - "Аналитической механике", открывшей новый этап в истории развития этой дисциплины. Широкое использование вариационного исчисления позволило Лагранжу объединить различные принципы статики и динамики, что естественным образом привело к обобщенным координатам, а затем и к уравнениям движения в форме, которая впоследствии получила наименование лагранжевой. Новая механика Лагранжа, впитавшая в себя силу методов математического анализа, оказалась не только способной решать те задачи, которые ставила бурно развивающаяся наука и техника тех дней, но и приспособленной к решению проблем, которые возникли в последующие времена, вплоть до сегодняшнего дня. На основе лагранжева учения развились впоследствии теоретические основы машиноведения, наука о сопротивлении материалов. Использованное в теории гироскопов, оно служит сегодня для стабилизации многочисленных сложных устройств, начиная с гироскопических компасов на кораблях, кончая системами автоматического управления космическими кораблями; на его основе рассчитываются траектории полета спутников. Это лишь некоторые, наудачу выбранные, примеры применения лагранжевой механики, но сказанного вполне достаточно, чтобы составить себе представление о том исключительном значении, которое она имела для последующего развития науки и техники. "Аналитическая механика" увидела свет уже в Париже, куда Лагранж переехал в 1787 г. (после смерти Фридриха II). Здесь он снова вернулся к преподавательской деятельности, вначале в Нормальной школе, созданной для подготовки преподавателей, а затем в знаменитой Политехнической школе, организованной с целью воспитания квалифицированных военных специалистов. Наряду с другими выдающимися преподавателями этих школ - Лапласом и Монжем - он много сделал для развития преподавания математики не только во Франции, но и во всей Европе. Опубликованный им курс элементарной математики, прочитанный в Нормальной школе, оказал большое влияние на всю учебную литературу того времени. Большое значение имела его деятельность для внедрения в школьное преподавание десятичных дробей, которые стали необходимым орудием вычислительной практики после реформы мер и весов, проведенной революционным французским правительством. (Кстати, сам Лагранж был членом комиссии, подготовившей эту реформу.) Прочитанный им курс математического анализа был опубликован впоследствии в двух книгах (1797, 1801 гг.) и содержал попытку обоснования математического анализа, в основах которого содержались в то время значительные неясности и пробелы (общепринятое сегодня обоснование было дано знаменитым французским математиком О. Л. Коши в 1821 г.). Говоря о научной деятельности Лагранжа, мы коснулись лишь некоторых ее аспектов, в то время как, подобно Эйлеру, Лагранж обогатил своим творчеством почти все области тогдашней математики. При этом целый ряд полученных им результатов по своей глубине и значению для развития математического знания ничуть не уступают его исследованиям по вариационному исчислению. Ему принадлежат фундаментальные результаты по алгебре (в частности, его работы по теории алгебраических уравнений послужили исходной точкой для исследований Э. Галуа), теории чисел (например, им была доказана теорема о том, что любое целое положительное число есть сумма не более чем четырех квадратов целых чисел), 'теории вероятностей, дифференциальным уравнениям, исчислению конечных разностей, комбинаторике, эллиптическим интегралам, различным вопросам математического естествознания и т. д. К сожалению, рассказать об этом, не выходя за рамки школьной математики, не представляется возможным. Во Франции Лагранж пережил Великую революцию, времена Директории, Консульства и, наконец, наполеоновскую Империю. Бурные исторические события нашли слабое отражение в его биографии. Сменявшие друг друга правительства с постоянным глубоким уважением относились к величайшему математику страны. Умер Жозеф Луи Лагранж в 1813 г. Человек слабого здоровья, удивительно деликатный в обращении, очень скромный, он прожил внешне неприметную, лишенную ярких биографических деталей жизнь - жизнь, наполненную вдохновенным творческим трудом, дыхание которой мы ощущаем и поныне. |
 |