Справочный отдел |
Летопись знаменательных дат развития математикиЗарождение математикиТочно датировать возникновение важнейших понятий - целого числа, величины, фигуры - невозможно. Когда возникла письменность, представление о них уже сложилось. К этому времени были выработаны и различные системы письменной нумерации целых чисел. 2000-1700 гг. до н. э. - первые дошедшие до нас математические тексты: два египетских папируса и многочисленные глиняные таблички из древнего Вавилона, содержащие формулировки и решения задач. Египтяне пользовались десятичной непозиционной нумерацией и дробями с числителем 1 ("основные" дроби). У вавилонян была шестидесятеричная позиционная система счисления без нуля и систематические шестидесятеричные дроби. Позднее, в середине первого тысячелетия до н. э. вавилоняне ввели знак для обозначения пропущенного шестидесятеричного разряда. Геометрия в Вавилоне и в Египте была по преимуществу вычислительной. Так, были известны правила вычисления площадей треугольника по стороне и высоте, круга по его радиусу (вавилоняне брали при этом в качестве Пи число 3, а египтяне - число 3,16), а также объемов пирамиды и усеченной пирамиды с квадратным основанием. Вавилоняне знали, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, а также обратное предложение. По-видимому, оба эти предложения были открыты ими на примерах и доказывать их в общем виде они еще не умели. Наиболее замечательное достижение этого периода -создание в древнем Вавилоне элементов алгебры и открытие правила решения квадратных уравнений. Вавилоняне умели также находить приближенные значения квадратных корней из неквадратных чисел. Им были известны правила суммирования арифметической прогрессии и ряда квадратов натуральных чисел. Математические знания излагались в эту эпоху в виде рецептов, правильность которых не доказывалась; обычно приводились однотипные числовые примеры и их решения. Математики как науки еще не было. Возникновение математики как науки. Построение первых математических теорий (математика Древней Греции)VI в. до н. э. - систематическое введение логических доказательств, явившееся переломным моментом в развитии математики. В Пифагорейской научной школе было начато построение геометрии как отвлеченной науки, истины которой выводятся из немногих исходных аксиом с помощью доказательств. К пифагорейцам восходят первые математические теории: планиметрия прямолинейных фигур (включая строгое доказательство знаменитой теоремы Пифагора) и элементы теории чисел (введение понятий простого числа, взаимно простых чисел, исследование делимости, построение совершенных чисел). В этой же школе были открыты три из пяти правильных тел: куб, тетраэдр и додекаэдр. V в. до н. э. - В Пифагорейской школе сделано величайшее открытие о несоизмеримости стороны квадрата и его диагонали. Оно показало, что рациональных чисел (т. е. целых чисел и дробей) недостаточно для измерения геометрических величин и обоснования учения о подобии. Благодаря этому открытию возникла необходимость создания теории отношений как соизмеримых, так и несоизмеримых величин. V в. до н. э. (вторая половина) - создана так называемая геометрическая алгебра, которая давала возможность в общем виде решать задачи, сводящиеся к квадратному уравнению или последовательности таких уравнений, чисто геометрически, с помощью циркуля и линейки. Геометрическая алгебра играла в античной математике роль нашей буквенной алгебры, но аппарат ее был гораздо менее удобен. В это же время были сформулированы три знаменитые задачи древности:
В поисках квадратуры круга Гиппократ Хиосский открыл квадрируемые луночки (получившие название гип-пократовых), т. е. фигуры, ограниченные дугами окружностей, для которых можно построить равновеликие им квадраты. В конце V в. Гиппократ составил первые "Начала" -систематическое изложение основ математики своего времени. Труд этот до нас не дошел. IV в. до н. э. (первая половина) - афинский математик Теэтет предпринял исследование алгебраических ир-рациональностей и начал классификацию их. Определил простейшие классы квадратичных иррациональностей, такие, как 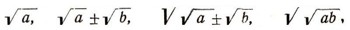 которые были впоследствии описаны в "Началах" Евклида. Он показал также, что три корня из а иррационален, если а не является кубом. Ему же принадлежит открытие октаэдра и икосаэдра. IV в. до н. э. (середина) - математик и астроном Евдокс из Книда создал общую теорию отношений для любых однородных величин (как соизмеримых, так и несоизмеримых). Эта теория совпадает, по существу, с теорией действительных чисел, предложенной в конце XIX в. Р. Дедекиндом. Для определения площадей и объемов Евдокс разработал так называемый "метод исчерпывания". В основе обеих теорий лежало общее учение о величинах, причем впервые была сформулирована важнейшая аксиома, известная ныне под названием аксиомы Архимеда: если a>b, то можно повторить bстолько раз, что nb>a. С помощью новых методов Евдокс впервые доказал, что конус равновелик 1/3 цилиндра, имеющего одинаковые с ним основания и высоту, а пирамида равновелика 1/3 соответствующей призмы. Он доказал также, что площади двух кругов относятся как квадраты их диаметров. 300 г. до н. э. - Евклид создал "Начала", в которых подвел итог всему предшествующему развитию античной математики. Дедуктивный метод изложения "Начал" стал образцом для построения математической теории. В "Началах" систематически изложены геометрия, элементы теории чисел, алгебры, теория отношений и метод исчерпывания. Здесь сформулирован алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, доказано, что произведение чисел ab делится на простое число р тогда и только тогда, когда один из сомножителей делится на р, а также, что простых чисел бесконечно много. В "Началах" впервые встречается строгий вывод формулы суммы конечного числа членов геометрической прогрессии и показывается, что существует только пять правильных многогранников: куб, тетраэдр, октаэдр, додекаэдр и икосаэдр. III в. до н. э. -Архимед разработал методы нахождения площадей и объемов, а также методы определения касательных и наибольших и наименьших значений величин, которые он применил для решения проблем статики, гидростатики и теории равновесия плавающих тел (см. стр. 436-438). Методы Архимеда легли в основу дифференциального и интегрального исчислений, созданных в XVII в. Архимед нашел все полуправильные многогранники. С помощью конических сечений он решал кубические уравнения вида x2(a±x)=b и проводил полное их исследование. III-II вв. до н. э. - Аполлоний систематически и всесторонне исследовал конические сечения. Его книги о конических сечениях послужили основой для создания аналитической геометрии Р. Декартом и П. Ферма (XVII в.), проективной геометрии В. Паскалем и Ж. Дезаргом (XVII в.), а также явились математическим аппаратом при исследованиях по механике и астрономии И. Кеплера, Г. Галилея и И. Ньютона. I-II вв. н. э. - широкое развитие вычислительно-алгебраических методов в античной математике. I в. (конец) - Менелай создал систематический курс сферической геометрии, построенный по образцу "Начал" Евклида, и развил сферическую тригонометрию. II в. - Птолемей в своих астрономических трудах изложил плоскую и сферическую тригонометрию; он вывел формулу, равносильную формуле sin (а± бета) = sin а . cos бета ± cos а * sin бета, и составил подробные таблицы хорд (вместо линии синуса древние рассматривали всю хорду). В таблицах Птолемей употреблял символ для обозначения пропущенного шестидесятеричного разряда. Возможно, что этот символ и явился прообразом нуля. III в. н. э. - Диофант Александрийский написал "Арифметику", в которой расширил числовую область до поля рациональных чисел, сформулировал правило умножения относительных чисел, ввел алгебраическую символику: знаки для первых шести положительных и отрицательных степеней неизвестного, для вычитания и равенства. Там же приведены и правила переноса членов из одной части уравнения в другую и приведения подобных. В "Арифметике" рассмотрены проблемы решения неопределенных уравнений в рациональных числах и даны методы для нахождения рациональных решений неопределенных уравнений второй и третьей степени. Математика стран Дальнего, Среднего и Ближнего ВостокаII в. до н. э. - создание древнейшего дошедшего до нас китайского математического трактата "Математика в девяти книгах", содержавшего сведения по арифметике и геометрии. При решении задач в трактате применялась теорема Пифагора. Наиболее замечателен в нем единообразный метод решения системы линейных уравнений. При этом появляются отрицательные числа, для которых формулируются правила сложения и вычитания. В трактате излагается также алгоритм вычисления квадратных и кубических корней, аналогичный современному. Этот алгоритм в VII-XIII вв. был перенесен на случай вычисления корней общих уравнений третьей и четвертой степеней. Он совпадает в основном с так называемой схемой Горнера, полученной в Европе в XIX в. III в. н. э. - в трактате Сунь Цзы встречаются именованные десятичные дроби. V-VI вв. - создание в Индии десятичной позиционной системы счисления и введение в нее нуля как особой дафры. 499 г. - в астрономическом трактате Ариабхата решил в целых числах неопределенное уравнение ах + bу=с. Около 628 г. - Брахмагупта, оперируя отрицательными числами, дал единое правило для решения любого квадратного уравнения, сформулировал правила действий с нулем, который благодаря этому стал числом, равноправным с другими числами. Брахмагупта пользовался алгебраической символикой: специальными знаками для неизвестных и их степеней, знаками для корня квадратного, для операций сложения и вычитания. IX в. - Мухаммед ал-Хорезми объяснил правила действий с числами, записанными в десятично-позиционной системе, и исследовал квадратные уравнения. Слова "алгебра" и "алгоритм" впервые появились в переводе его трактатов. Первое из них означало операцию переноса членов из одной части уравнения в другую, а второе -искаженное имя автора (ал-Хорезми - Algorithmi), оно применялось первоначально только для обозначения правил вычисления по десятичной позиционной системе. XI в. - математик и поэт Омар Хайям в трактате по алгебре решал геометрически кубические уравнения (по методу Архимеда). Комментируя "Начала" Евклида, он сблизил понятия отношения и числа. Ко времени Хайяма была известна формула возведения бинома в любую целую положительную степень и способ извлечения корня любой степени. XII в. - Бхаскара-акарья сформулировал все правила действий с отрицательными числами. Бхаскара знал, что благодаря двузначности квадратного корня квадратное уравнение может иметь два решения. XIII в. - Насирэддин Туси написал трактат по сферической геометрии и тригонометрии, содержавший учение о решении треугольников. Трактат сыграл решающую роль для развития тригонометрии в Европе. XV в. - Джемшид ал-Каши, работавший в обсерватории Улугбека близ Самарканда, ввел и применял десятичные дроби: десятичная позиционная система была распространена на запись любых действительных чисел. Он вычислил число л с точностью до 17 десятичных знаков. Математика европейского средневековья и эпохи ВозрожденияXII-XIII вв. - на латинский язык переведены арабские и греческие сочинения по математике. Постепенно в Европе распространилась десятичная позиционная система. XIII в. - Леонардо Пизанский (Фибоначчи) изложил нов'ую позиционную нумерацию, дал сведения по алгебре и арифметике, рассмотрел различные числовые ряды. XIV-XV вв. - усовершенствована алгебраическая символика, введены обозначения для степени, для радикала и степеней неизвестного. XVI в. - первый крупный успех европейской математики : С. Ферро, Н. Тарталья и Дж. Кардано решили уравнение третьей степени в радикалах и ученик Кардано, Л. Феррари, - уравнение четвертой степени. 1572 г. - в "Алгебре" Р. Бомбелли впервые рассмотрел мнимые числа a+b корень из -1 и сформулировал правила действий с ними. Сами эти числа он трактовал как символы, удобные для получения результатов относительно действительных чисел. 1585 г. - С. Стевин ввел десятичные дроби. XVI в. (вторая половина) - Ф. Виет ввел буквенные обозначения для неизвестных и постоянных величин и создал математическую формулу. Период математики переменных величин [XVII-XVIII вв.]В XVII в. сделала большие успехи механика земных и небесных тел, и в связи с этим возникли проблемы изучения зависимостей одних величин от других, проблемы определения скоростей, ускорений, площадей криволинейных фигур, центров тяжести и т. д. Для решения этих проблем в математике не было готового аналитического аппарата. Ученые начали искать пути изучения переменных величин в математике, используя творения античных математиков. В результате функция (термин Г. Лейбница) стала таким же основным объектом математики, как число и величина. 1614 г. - Дж. Непер ввел логарифмы и опубликовал первые логарифмические таблицы. Несколько позднее таблицы логарифмов опубликовал И. Бюрги. 1636-1637 гг. - Р. Декарт и П. Ферма ввели в математику метод координат, который позволил сводить геометрические задачи к алгебраическим. Независимо друг от друга Декарт и Ферма строили с помощью нового метода аналитическую геометрию. Декарт придал алгебраической символике современный вид. 1608-1660 гг. - развитие анализа бесконечно малых (методов определения объемов, площадей, центров тяжестей, касательных, экстремумов, скоростей, ускорений) в работах И. Кеплера, Б. Кавальери, Э. Торричелли, П. Ферма, Б. Паскаля, Дж. Валлиса, И. Барроу и др. 40-50-е годы XVII в. - П. Ферма сформулировал знаменитые проблемы теории чисел, которые в течение 200 лет оставались центральными в этой науке. 1665 г. - Б. Паскаль в "Трактате об арифметическом треугольнике", выводя свойства биномиальных коэффициентов и соотношения между ними, сформулировал и применил принцип полной математической индукции. 60-80-е годы XVII в. - И. Ньютон (с 1665 г.) и Г. Лейбниц (с 1673 г.) независимо друг от друга создали дифференциальное и интегральное исчисления и ввели в математику важнейший аналитический аппарат для представления и изучения функций - степенные ряды. Ньютон распространил формулу возведения бинома в степень на случай, когда показатель есть любое рациональное число. 1687 г. - вышла в свет книга И. Ньютона "Математические начала натуральной философии", в которой было дано математическое построение основ классической механики земных и небесных тел. 1713 г. - вышло в свет (посмертно) сочинение Я. Бернулли, содержащее простейшую форму закона больших чисел - одного из основных законов теории вероятностей. 40-е годы XVIII в. - Л. Эйлер развил учение о функциях как действительного, так и комплексного переменного. Он подробно исследовал элементарные функции хn, an log x, sin x, cos x, нашел для них выражения в виде бесконечных рядов и определил логарифмы отрицательных и мнимых чисел. 30-60-е годы XVIII в. - Л. Эйлер доказал основные теоремы элементарной теории чисел, исследовал квадратичные вычеты и открыл квадратичный закон взаимности - один из основных в высшей арифметике. Эйлер доказал частный случай великой теоремы Ферма, а именно что уравнение 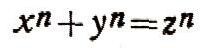 при n=3 и n=4 не имели решений в целых числах. При этом он рассматривал выражения вида m+n корень из -3 как новые целые числа, что было первым обобщением понятия целого числа. 1770-1771 гг, - Ж. Лагранж проанализировал все методы решения в радикалах уравнений первых четырех степеней и показал, почему все эти методы не годятся для решения уравнений пятой степени. Он открыл, что разрешимость уравнений в радикалах зависит от свойств группы перестановок корней этого уравнения, и тем самым обратил внимание на значение изучения групп. 1796 г. - К. Гаусс показал, что если п - простое число, то правильный и-угольник может быть построен с помощью циркуля и линейки, когда п имеет вид 22к + 1 (см. стр. 453-456). 1799 г. - К. Вессель дал геометрическую интерпретацию комплексных чисел. Однако его работы остались неизвестными. В 1806 г. аналогичная геометрическая интерпретация была предложена Ж. Арганом. Всеобщее признание в математике комплексные числа получили только после работ К. Гаусса в 1832 г. Период современной математики (XIX-XX вв.)Математические методы проникли почти во все отделы физики, в химию, а в последние десятилетия - в биологию, медицину, лингвистику, экономику. Сама математика необыкновенно расширилась количественно и претерпела глубокие качественные изменения. В целом она поднялась на более высокую ступень абстракции. 1801 г. - К, Гаусс создал основы теории чисел. Он впервые развил теорию сравнений, доказал основные теоремы этой теории, изучил до конца теорию квадратичных вычетов, изложил теорию уравнений деления круга. 1821--1823 гг. - О. Коши развил теорию пределов и на основе ее построил учение о функциях, определил понятие суммы ряда, непрерывности функции, а поздней учение о пределах положил в основу всего математического анализа. Коши принадлежит также разработка основ теории функций комплексного переменного (1825). 1824-1826 гг. - Н. Абель доказал, что алгебраические уравнения степени n > 5 в общем виде неразрешимы в радикалах. 1827 г. - К. Гаусс развил так называемую внутреннюю геометрию поверхностей, в которой каждая поверхность выступает как носительница свойств особой геометрии. 1829-1830 гг. - Н. И. Лобачевский опубликовал свои первые работы по неевклидовой геометрии, которые открыли новую эру в истории геометрии. Независимо от Н. И. Лобачевского систему неевклидовой геометрии построил Я. Больяй (1831). 1830-1832 гг. - Э. Галуа нашел критерий того, решается ли данное уравнение с числовыми коэффициентами в радикалах. При этом он развил методы теории групп и полей, которые приобрели огромное значение в математике и ее приложениях. 1832 г. - в связи со своими исследованиями по теории чисел К. Гаусс распространил понятие целого числа на комплексные числа а + bi, где а и b - целые. Перенес на новые числа алгоритм нахождения наибольшего общего делителя и развил всю арифметику целых комплексных чисел. 1840-1851 гг. - У. Гамильтон обобщил понятие комплексного числа, построив кватернионы - числа вида a + bi+cj+dk, где i2=j2=k2=-1; а, b, с, d - действительные числа. Оказалось, что для этих чисел выполняются уже не все законы обычной арифметики. Так, умножение кватернионов не обладает свойством переместительности ij не равно ji. 1847 г. - Э. Куммер при помощи введения так называемых идеальных чисел построил арифметику целых чисел полей деления круга. Это дало ему возможность доказать великую теорему Ферма для всех n<100). 1849 г. - П. Л. Чебышёв получил первые после Евклида точные результаты о распределении простых чисел в натуральном ряду (см. стр. 458-460). 1854 г. - Б. Риман, обобщая идеи Гаусса по внутренней геометрии поверхностей, дал способ построения всевозможных метрических неевклидовых геометрий. Римановы геометрии стали впоследствии основным математическим аппаратом общей теории относительности. Частным случаем римановых геометрий являются геометрия Евклида и геометрия Лобачевского. 1871-1889 гг. - Р. Дедекинд, Е. И. Золотарев и Л. Кронекер независимо друг от друга и разными методами построили арифметику целых чисел любого поля алгебраических чисел. При этом Дедекинд ввел с помощью систем аксиом такие основные понятия современной алгебры, как кольцо, модуль и идеал. 1881-1882 гг. - Р. Дедекинд, Г. Кантор и К. Вейерштрасс построили тремя различными способами теорию действительных чисел. Вскоре в работах Дедекинда и особенно Кантора возникла новая важная область современной математики - теория множеств. 1899 г. - Д. Гильберт в "Основаниях геометрии" построил полную аксиоматику геометрии Евклида и проанализировал соотношения между различными группами аксиом. С этого времени большое развитие в математике получил аксиоматический метод. XX в. - созданы новые математические теории, как например, топология, математическая логика, и коренным образом преобразованы старые, изменился сам язык математики, так что математику XIX в. для чтения современных книг пришлось бы переучиваться заново. Понятия, методы и конструкции современной математики носят весьма общий характер. Соответственно чрезвычайно расширилось поле применения математических методов. |
 |