- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядкаДипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядкаМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Учреждение образования "Гомельский государственный университет имени Франциска Скорины" Математический факультет Кафедра дифференциальных уравнений Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка Дипломная работа Исполнитель: студентка группы М-51 БРАВАЯ Е.Н. Научный руководитель: доцент, к. ф-м. н. ФИЛИПЦОВ В.Ф. Рецензент: профессор, д. ф-м. н. СТАРОВОЙТОВ Э.И. Гомель 2003 РефератДипломная работа 38 страниц, 11 источников. Ключевые слова и словосочетания: квадратичная двумерная стационарная система, частный интеграл, парабола, гипербола, окружность, точка, характеристическое уравнение, характеристическое число, узел, седло, фокус. Данная работа содержит результаты исследований автора, относящиеся к качественному исследованию в целом двумерной квадратичной стационарной системы. Основным инструментом исследований является понятие частного интеграла. Работа состоит из двух глав. В первой главе проводится построение квадратичных двумерных стационарных систем с заданными интегралами, при этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя соотношениями. Во второй главе проводится качественное исследование в целом выделенных в первой главе классов систем при фиксированных значениях некоторых параметров. Содержание Реферат Введение 1. Построение квадратичных двумерных стационарных систем 1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде параболы 1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде окружности либо гиперболы 1.3 Необходимые и достаточные условия существования у системы (1.1) двух частных интегралов (1.3), (1.13) 2. Качественное исследование построенных классов систем 2.1 Исследование системы (1.1) с коэффициентами, заданными формулами (1.28) - (1.31) 2.2 Исследование системы (1.1) с коэффициентами, заданными формулами (1.41) - (1.42) 2.3 Исследование системы (1.1) с коэффициентами, заданными формулами (1.52) - (1.53) Заключение Список использованных источников Приложение А Приложение Б Приложение В ВведениеИзвестно, что в элементарных функциях и даже в квадратурах интегрируются очень немногие классы дифференциальных уравнений. В связи с этим появилась необходимость в создании такой теории, с помощью которой можно было бы изучать свойства решений дифференциальных уравнений по виду самих уравнений. Такой теорией, наряду с аналитической, и является качественная теория дифференциальных уравнений. Впервые задача качественного исследования для простейшего случая системы двух дифференциальных уравнений с полной отчетливостью была поставлена А. Пуанкаре [7] в конце прошлого столетия. Позднее исследования А. Пуанкаре были дополнены И. Бендиксоном [3, с. 191-211] и уточнены Дж.Д. Биркгофом [4, с.175-179].
Одной из задач качественной теории дифференциальных уравнений является изучение поведения траекторий динамической системы (0.1) на фазовой плоскости в целом в случае, когда P (x,y) и Q (x,y) - аналитические функции. Интерес к изучению этой системы или соответствующего ей уравнения объясняется их непосредственным практическим применением в различных областях физики и техники.
Имеется много работ, в которых динамические системы изучались в предположении, что их частными интегралами являются алгебраические кривые. Толчком к большинству из них послужила работа Н.П. Еругина [6, с.659 - 670], в которой он дал способ построения систем дифференциальных уравнений, имеющих в качестве своего частного интеграла кривую заданного вида. Знание одного частного алгебраического интеграла системы (0.1) во многих случаях помогает построить полную качественную картину поведения интегральных кривых в целом. Отметим ряд работ этого характера для систем (0.1), в которых P (x,y) и Q (x,y) - полиномы второй степени. Н.Н. Баутиным [1, с.181 - 196] и Н.Н. Серебряковой [8, с.160 - 166] полностью исследован характер поведения траекторий системы (0.1), имеющей два алгебраических интеграла в виде прямых. В [10, с.732 - 735] Л.А. Черкасом такое исследование проведено для уравнения (0.2) при наличии частного интеграла в виде кривой третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система
и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая распадается на две кривые второго порядка, одна из которых парабола, вторая окружность или гипербола. Работа состоит из двух глав. В первой главе проводится построение квадратичных двумерных стационарных систем с заданными интегралами, при этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя соотношениями. Во второй главе проводится качественное исследование в целом выделенных в первой главе классов систем при фиксированных значениях некоторых параметров. 1. Построение квадратичных двумерных стационарных систем1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде параболыРассмотрим систему дифференциальных уравнений
Пусть система (1.1) имеет частный интеграл вида:
где Fk (x,y) - однородные полиномы от x и y степени k. В качестве частного интеграла (1.2) возьмем параболу вида: F (x,y) º y+a1 x2 +a2 x+a3 = 0 (1.3) Будем предполагать, что a3 ¹ 0, то есть парабола не проходит через начало координат. Согласно [10, с.1752-1760] для интеграла (1.3) системы (1.1) имеет место соотношение:
где L (x,y) = px+my+n, p, m, n - постоянные. Тогда следуя формуле (1.4) получим равенство: (2a1x+a2) (ax+by+a1x2+2b1xy+c1y2) + (cx+dy+a2x2+2b2xy+c2y2) = = (y+a1x2+a2x+a3) (px+my+n). Приравнивая коэффициенты при одинаковых степенях xm yn слева и справа, получим равенства: (2a1-p) a1= 0 (1.51) (4b1-m) a1= 0 (1.52) 2a1c1= 0 (1.53) (2a-n) a1+ (a1-p) a2+a2= 0 (1.61) 2a1b+ (2b1-m) a2+2b2+p= 0 (1.62) a2c1+c2-m= 0 (1.63) (a-n) a2-pa3n+c= 0 (1.71) a2b-a3m+d-n= 0 (1.72) a3n= 0 (1.73) Пусть a1¹ 0, тогда из равенств (1.51), (1.52), (1.53), (1.63) и (1.73) получаем, что P=2a1, m=4b1, c1=0, c2=4b1, n=0 (1.8) Из соотношений (1.61), (1.62) и (1.71) найдем выражения коэффициентов кривой (1.3) через коэффициенты системы (1.1) в следующем виде: a1 a2 a3 Равенство (1.72) с учетом полученных выражений (1.9) - (1.11), даст условие, связывающее коэффициенты a, b, c, d, a1, a2, b1, b2:
Итак, установлена следующая теорема: Теорема 1.1 Система (1.1) имеет частный интеграл (1.3), коэффициенты которого выражаются формулами (1.9) - (1.11), при условии, что коэффициенты системы связаны соотношением (1.12) и c1= 0, c2= 4b1, a1¹0, 2b1a-a1b¹0. 1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде окружности либо гиперболыПусть теперь система (1.1) наряду с интегралом (1.3) имеет интеграл в виде: y2+sx2+bx+gy+d=0 (1.13) Будем рассматривать теперь систему:
Согласно формуле (1.4), где L (x,y) = m1x+n1y+p1, m1, n1, p1 - постоянные для системы (1.1), имеем: (2a1-m1) s2= 0 (1.151) (4b1-n1) s+2a1= 0 (1.152) m1= 4b2 (1.153) n1=8b1 (1.154) (2a-p1) s+ (a1-m1) b+a2g=0 (1.161) 2bs+ (2b1-n1) b+ (2b2-m1) g+2c= 0 (1.162) (4b1-n1) g+2d-p1= 0 (1.163) (a-p1) b+cg+m1d= 0 (1.171) bb+ (d-p1) g-n1d= 0 (1.172) p1d= 0 (1.173) Предположим, что кривая не проходит через начало координат, то есть d¹0. Пусть s¹0, тогда из равенств (1.151), (1.153), (1.154) и (1.173) получаем, что m1=4b2, n1=8b1, a1=2b2, p1=0 (1.18) А из соотношений (1.161), (1.163) и (1.171) найдем выражения коэффициентов кривой (1.13) через коэффициенты системы (1.1) в следующем виде:
Подставляя коэффициенты s, b, g и d в равенства (1.162) и (1.172), получим два условия, связывающие коэффициенты a, b, c, d, a2, b1, b2:
Итак, установлена следующая теорема: Теорема 1.2 Система (1.14) имеет частный интеграл (1.13), коэффициенты которого выражаются формулами (1.19) - (1.22), при условии, что коэффициенты системы связаны соотношениями (1.23), (1.24) и b1¹0, b2¹0, a1=2b2. 1.3 Необходимые и достаточные условия существования у системы (1.1) двух частных интегралов (1.3), (1.13)В разделах 1.1-1.2 мы получили, что система (1.1) будет иметь два частных интеграла в виде кривых второго порядка при условии, что коэффициенты системы связаны соотношениями:
Причем b1¹0, b2¹0, a1¹0, b1a-b2b¹0. Выражая c из первого уравнения системы (1.25), получим
Подставим (1.26) во второе и третье уравнения системы (1.25). Получим два соотношения, связывающие параметры a, b, d, a2, b1, b2:
Пусть
Из первого уравнения системы (1.27) получим
Подставляя
Из соотношений (1.25) при условиях (1.27) получаем, что коэффициенты системы (1.1) определяются следующими формулами:
Равенства (1.9) - (1.11), (1.19) - (1.22) при условии, что имеют место формулы (1.28) - (1.31), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.13): a1 a2 a3 s b g d Теорема 1.3 Система (1.1) имеет частные интегралы вида (1.3) и (1.13) с коэффициентами, определенными формулами (1.32) - (1.38), при условии, что коэффициенты системы (1.1) выражаются через параметры по формулам (1.28) - (1.31). Пусть
Из первого уравнения системы (1.39) найдем
Подставляя
Поскольку
Из соотношений (1.25) при условиях (1.39) и (1.40) получаем, что коэффициенты системы (1.1) определяются следующими формулами:
Равенства (1.9) - (1.11), (1.19) - (1.22) при условии, что имеют место формулы (1.41) - (1.42), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.13): a1 a2 a3 s b=0 (1.47) g d Теорема 1.4 Система (1.1) имеет частные интегралы вида (1.3) и (1.13) с коэффициентами, определенными формулами (1.43) - (1.49), при условии, что коэффициенты системы (1.1) выражаются через параметры по формулам (1.41) - (1.42). б)
Из (1.50) найдем
Из соотношений (1.25) при условиях (1.39) и (1.50) - (1.51) получаем, что коэффициенты системы (1.1) определяются следующими формулами:
Равенства (1.9) - (1.11) и (1.19) - (1.22) при условии, что имеют место формулы (1.52) - (1.53), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.13): a1=0 (1.54) a2 a s b g d Теорема 1.5 Система (1.1) имеет частные интегралы вида (1.3) и (1.13) с коэффициентами, определенными формулами (1.54) - (1.60), при условии, что коэффициенты системы (1.1) выражаются через параметры по формулам (1.52) - (1.53). 2. Качественное исследование построенных классов систем2.1 Исследование системы (1.1) с коэффициентами, заданными формулами (1.28) - (1.31)Будем проводить наше
исследование в предположении, что Пусть мы имеем систему (1.1), коэффициенты которой определяются согласно формулам (1.28) - (1.31), тогда система (1.1) запишется в виде:
Интегральные кривые в этом случае имеют вид:
Найдем состояния равновесия системы (2.1). Приравняв правые части системы нулю и исключив переменную y, получим следующее уравнение для определения абсцисс состояний равновесия:
Из (2.4) получаем, что
Ординаты точек покоя имеют вид:
Итак, имеем точки
Исследуем поведение
траекторий в окрестностях состояний равновесия Исследуем точку Составим характеристическое
уравнение в точке
Отсюда
Следовательно, характеристическое уравнение примет вид:
Или
Характеристическими числами
для точки
Корни Исследуем точку
Составим характеристическое уравнение в точке
Согласно равенствам (2.5) характеристическое уравнение примет вид:
Или
Характеристическими числами
для точки
то есть
Корни
неустойчивый узел, если d>0, то точка
устойчивый узел. Исследуем точку Применяя равенства (2.5), составим характеристическое уравнение в точке
Характеристическими числами для точки
системы (2.1) будут
то есть
Корни Исследуем точку
Составим характеристическое уравнение в точке
Применяя равенства (2.5), получим:
Или
Характеристическими числами для точки
системы (2.1) будут
то есть
Корни
седло. Исследуем бесконечно - удаленную часть плоскости в конце оси oy. Преобразование
переводит систему (2.1) в систему:
где Для исследования состояний
равновесий на концах оси y, нам необходимо исследовать только точку
Получим, что
Корни Исследуем бесконечно - удаленную
часть плоскости вне концов оси oy преобразованием [7]
где Изучим бесконечно - удаленные точки на оси U, то есть при z=0. Имеем:
Получаем, что Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 1. Таблица 1.
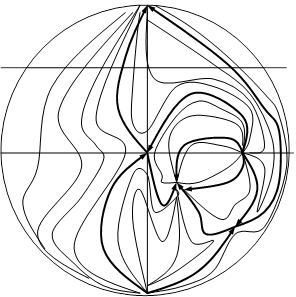
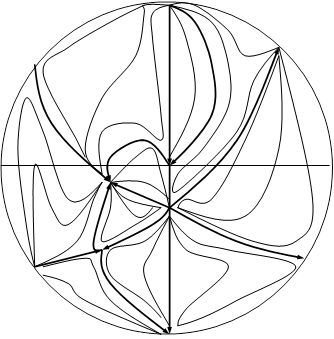
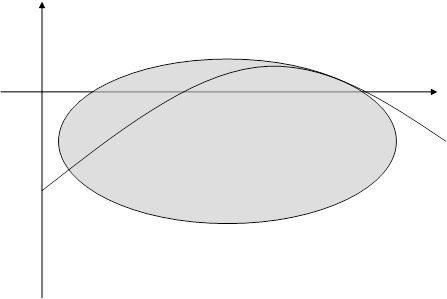
Положение кривых (2.2), (2.3) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.1 (а, б). Поведение траекторий системы в целом при d<0 и d>0 дается рис.4 (а, б) приложения А: Поведение траекторий системы (2.1). Исследуя вид кривых (2), (2.3) и расположение относительно их состояний равновесия, убеждаемся, что система (2.1) не имеет предельных циклов, так как Воробьев А.П. [5] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса. Учитывая расположение состояний равновесия относительно кривых (1.3) и (1.13), являющиеся интегралами системы (2.1), характер состояния, заключаем, что для системы (2.1) не может существовать предельных циклов, окружающих несколько состояний равновесия.
а (d<0)
б (d>0) Рис. 1 2.2 Исследование системы (1.1) с коэффициентами, заданными формулами (1.41) - (1.42)Будем проводить наше исследование в предположении, что
Пусть мы имеем систему (1.1), коэффициенты которой определяются формулами (1.41) - (1.42). Тогда система (1.1) будет иметь вид:
Интегральные кривые в этом случае имеют вид:
Частный интеграл (1.13) в этом случае преобразовывается в две прямые (2.10) 1. Найдем состояния равновесия системы (2.8). Для этого приравняем правые части системы нулю
Рассмотрим два случая:
Получаем:
Из первого уравнения найдем y:
и подставляя y во второе уравнение получим:
Решая это уравнение, находим:
Итак, получаем
Итак, получаем точки
и прямую x=0, которая является траекторией системы (2.8). 2. Исследуем поведение
траекторий в окрестностях состояний равновесия Исследуем точку Составим характеристическое
уравнение в точке
Отсюда
Следовательно, характеристическое уравнение примет вид:
Характеристическими числами
для точки
Корни Исследуем точку Согласно (2.11) составим
характеристическое уравнение в точке
Характеристическими числами
для точки
Корни 3. Исследуем поведение
траекторий в окрестности точки Составим характеристическое уравнение согласно (2.11)
Характеристическими числами
для точки
Корни 4. Исследуем поведение
траекторий в окрестности точки Согласно (2.11) составим характеристическое уравнение:
Характеристическими числами
для точки
Корни Исследуем бесконечно - удаленную
часть плоскости системы (2.8) вне концов оси oy. Преобразование
[7]
где Изучим бесконечно - удаленные точки на оси U, то есть при z=0. Получаем:
Следовательно Таким образом, получаем две точки N1 (0,-1) и N2 (0,1), которые являются состоянием равновесия. Исследуем характер этих точек обычным способом. Составим характеристическое уравнение в точке N1 (0,-1).
Имеем:
Корни Исследуем точку N2 (0,1). Согласно (2.13) составим характеристическое уравнение:
Корни Исследуем концы оси y с
помощью преобразования [7]
где Для исследования состояний равновесия на концах оси y, нам необходимо исследовать только точку N3 (0,0). Составим характеристическое уравнение в точке N3 (0,0):
Корни Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 2. Таблица 2.
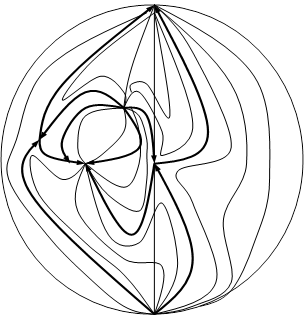
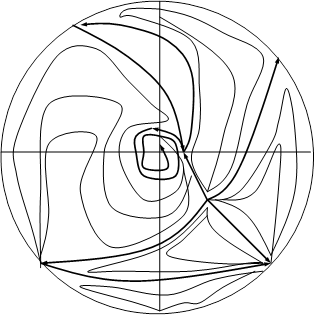
Положение кривых (2.9), (2.10) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.2 (а, б). Поведение траекторий системы в целом при d<0 и d>0 дается рис.5 (а, б) приложения Б: Поведение траекторий системы (2.8). Вопрос о существовании предельных циклов не возникает, так как Воробьев А.П. [5] доказал, для квадратичной системы предельный цикл не может окружать узел.
а (d<0) б (d>0) Рис. 2 2.3 Исследование системы (1.1) с коэффициентами, заданными формулами (1.52) - (1.53)Будем проводить наше исследование в предположении, что
Пусть мы имеем систему (1.1), коэффициенты которой определяются формулами (1.52) - (1.53). Тогда система (1.1) будет иметь вид:
Интегральные кривые в этом случае имеют вид:
То есть частные интегралы (1.3) и (1.13) преобразовываются в прямые таким образом, что интегральная кривая (2.16) совпадает с одной из прямых интегральной кривой (2.17). Найдем состояния равновесия системы (2.15). Приравняв правые части системы нулю, и исключив переменную y, получим следующее уравнение для определения абсцисс состояний равновесия:
Из (2.18) получаем, что
Ординаты точек покоя имеют вид:
Итак, имеем точки
Исследуем поведения
траекторий в окрестностях состояний равновесия Исследуем состояние
равновесия в точке Составим характеристическое уравнение.
Отсюда
Следовательно, характеристическое уравнение примет вид
Имеем
Или
Характеристическими числами
для точки
Корни Исследуем точку
Согласно (2.19) составим характеристическое уравнение в точке
Имеем
Характеристическими числами
для точки
Корни 3. Исследуем точку По (2.19) составим
характеристическое уравнение в точке Получим
Решая уравнение, получим
то есть
Корни Исследуем бесконечно - удаленную
часть плоскости вне концов оси oy преобразованием [7]
где Изучим бесконечно - удаленные точки на оси u, то есть при z=0. Получаем
Следовательно Итак, имеем две точки N1 (0,2) и N2 (0,-2). Исследуем характер этих точек обычным способом. Составим характеристическое уравнение в точке N1 (0,2).
Следовательно
Воспользуемся параллельным переносом
и подставим z, u в систему (2.20). Получим новую систему:
Составим характеристическое уравнение в точке N2 (0,-2)
Характеристическими числами для точки N2 (0,-2), будут
сложное состояние равновесия. Для определения характера состояния равновесия воспользуемся теоремой [2, с. 196-198]. Теорема 2.1. Пусть точка (0,0) - изолированное состояние равновесия системы:
где
Тогда 1) при m - нечетном
и при m - нечетном и при m - четном точка (0,0) есть седло - узел, то есть такое состояние равновесия, каноническая окрестность которого состоит из параболистического и двух гиперболических секторов. При этом если если Чтобы воспользоваться теоремой, необходимо систему (2.22) привести к виду:
Это можно сделать, воспользовавшись одним из следующих преобразований [2, с. 199-201]: если если если где a, b, c, d - коэффициенты системы (2.23). Тогда для системы (2.22) возьмем следующее преобразование:
Получим
Тогда
Найдем решение уравнения:
в виде ряда по степеням Z1:
Следовательно
Тогда
Подставляя U1 в систему (2.24) получим:
Отсюда
Следовательно, по теореме 2.1 получаем, что точка N2 (0,-2) - седло - узел. Исследуем концы оси y с
помощью преобразования [7]
где Для исследования состояний равновесий на концах оси y, нам необходимо исследовать только точку N3 (0,0). Составим характеристическое уравнение в точке N3 (0,0)
Соответственно характеристическими числами будут
Корни Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 3. Таблица 3.
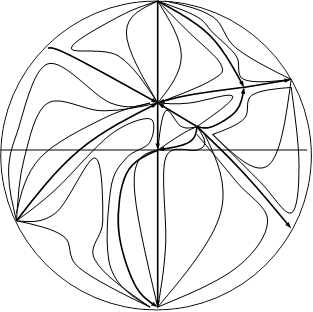
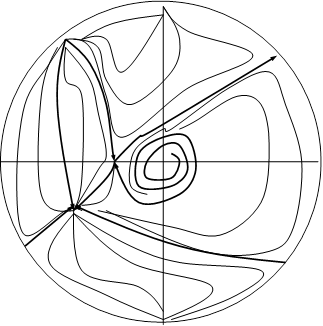
Положение кривых (2.16), (2.17) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.3 (а, б). Поведение траекторий системы в целом при d<0 и d>0 дается Рис.6 (а, б) приложения В: Поведение траекторий системы (2.15). Вопрос существования предельных циклов остается открытым.
а (d<0)
б (d>0) Рис. 3 ЗаключениеВ данной дипломной работе построена квадратичная двумерная стационарная система при условии, что частным интегралом является кривая четвертого порядка, которая распадается на две кривые второго порядка, одна из которых парабола, вторая окружность или гипербола. При этом коэффициенты кривых выражаются через произвольный параметр системы. Проведено качественное исследование системы. Найдены необходимые и достаточные условия существования у системы двух частных интегралов. В зависимости от коэффициентов были рассмотрены 3 случая. Найдены состояния равновесия трех полученных систем, которые принадлежат интегральным кривым. Исследована бесконечно-удаленная часть плоскости систем, в двух из которых доказано отсутствие предельных циклов. Выяснено поведение сепаратрис седел и построена качественная картина поведения траекторий систем в круге Пуанкаре. Список использованных источников1. Баутин Н.Н. О числе предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра // Матем. сб. - 1952. - Т.30,№1. - 458 с. 2. Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. - М.: Наука, 1976. - 274 с. 3. Бендиксон И. О кривых, определяемых дифференциальными уравнениями. - УМН, 1941. - Вып.9. - 643 с. 4. Биркгоф Дж.Д. Динамические системы. М. - Л.: Гостехиздат, 1941. - 340 с. 5. Воробьев А.П. К вопросу о циклах вокруг особой точки типа “узел" // ДАН БССР. - 1960. - Т.4,№9. - 720 с. 6. Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую. - ПММ. - 1952. - Т.16, Вып.6. - с.659-670. 7. Пуанкаре А. О кривых, определяемых дифференциальными уравнениями. - М. - Л.: ГИТТЛ, 1947. - 839 с. 8. Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний. - ПММ. - 1963 Т.27, Вып.1. - 230 с. 9. Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения. - 1973. - Т.9,№3. - 256 с. 10.
Черкас Л.А. Об алгебраических решениях уравнения 11. Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения. - 1970. - Т.6,№10. - с.1752-1760. Приложение АПоведение траекторий системы (2.1)
а) (d<0)
б) (d>0) Рис. 4 Приложение БПоведение траекторий системы (2.8)
а) (d<0)
б) (d>0) Рис. 5 Приложение ВПоведение траекторий системы (2.15)
а) (d<0)
б) (d>0) Рис. 6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
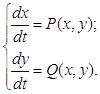 (0.1)
(0.1)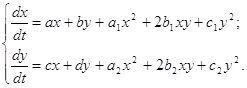 (0.3)
(0.3)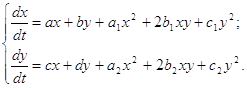 (1.1)
(1.1)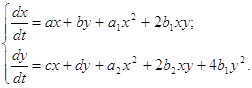 (1.14)
(1.14)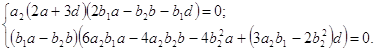
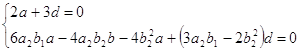 (1.27)
(1.27)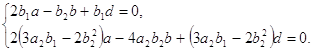 (1.39)
(1.39)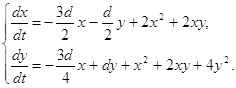 (2.1)
(2.1)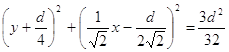 (2.3)
(2.3)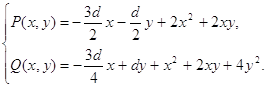
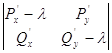 =
=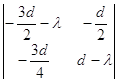 =0.
=0.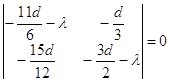
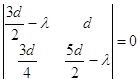
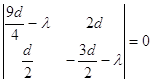
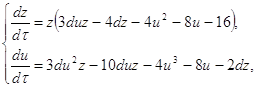 (2.6)
(2.6)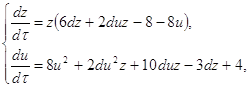 (2.7)
(2.7)
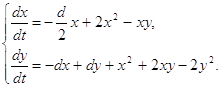 (2.8)
(2.8)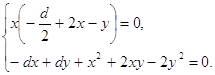
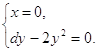
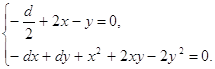
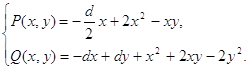
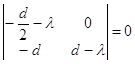
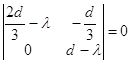 .
.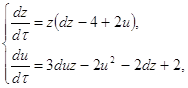 (2.12)
(2.12)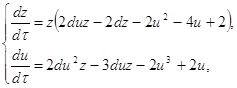 (2.14)
(2.14)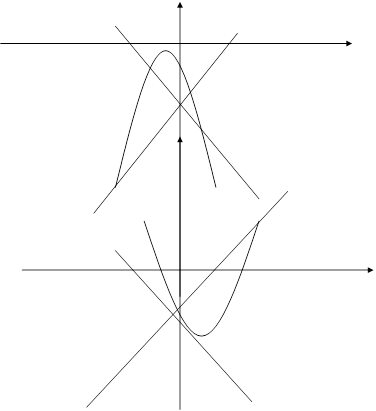
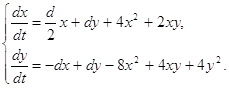 (2.15)
(2.15)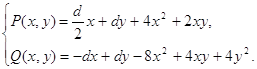
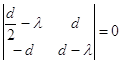
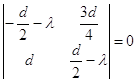 .
.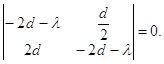
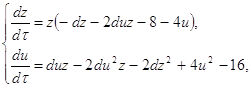 (2.20)
(2.20)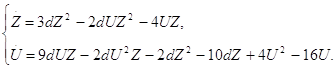 (2.22)
(2.22)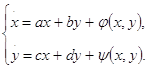 (2.23)
(2.23)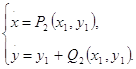
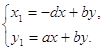
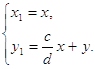
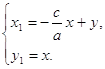
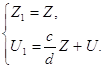
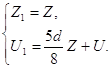
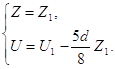
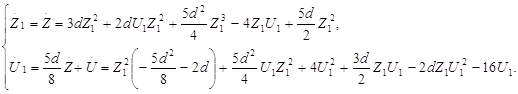 (2.24)
(2.24)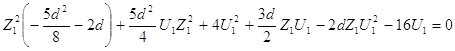
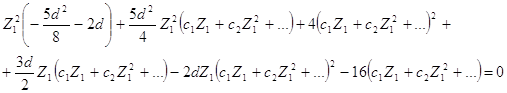
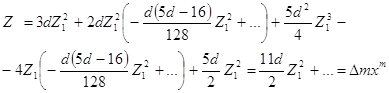
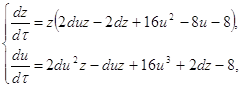 (2.25)
(2.25)