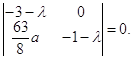- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых третьего и первого порядковДипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых третьего и первого порядковМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Учреждение образования «Гомельский государственный университет имени Франциска Скорины» Математический факультет Кафедра дифференциальных уравнений Допущена к защите Зав. кафедрой____________Мироненко В. И. «____»_________________ 2003 г. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ В ЦЕЛОМ ДВУМЕРНОЙ КВАДРАТИЧНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ С ДВУМЯ ЧАСТНЫМИ ИНТЕГРАЛАМИ В ВИДЕ КРИВЫХ ТРЕТЬЕГО И ПЕРВОГО ПОРЯДКОВ Дипломная работа Исполнитель: студентка группы М-51 _____________________ ПЛИКУС Т.Е. Научный руководитель: доцент, к.ф-м.н. _____________________ ФИЛИПЦОВ В.Ф. Рецензент:доцент, к.ф-м.н. _____________________ РУЖИЦКАЯ Е.А. Гомель 2003
Дипломная работа состоит из 25 страниц, 11 источников. Ключевые слова и словосочетания: квадратичная двумерная стационарная система, частный интеграл, кривые третьего и первого порядков, точка, характеристическое уравнение, характеристическое число, узел, седло. Объект исследования: квадратичная двумерная стационарная система с заданными интегральными кривыми третьего и первого порядков. Предмет исследования: построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков, нахождение и исследование состояний равновесия, исследование бесконечно-удаленной части плоскости. Цель дипломной работы: качественное исследование в целом двумерной квадратичной стационарной системы. Основным инструментом исследований является понятие частного интеграла.
Введение 1 Построение квадратичных двумерных стационарных систем 1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой третьего порядка 1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой первого порядка 1.3 Необходимые и достаточные условия существования у системы (1.1) двух частных интегралов (1.4), (1.18) 2 Исследование поведения траекторий системы на плоскости 2.1 Исследование системы (1.1) с коэффициентами, заданными формулами (1.35) в конечной плоскости2.2 Исследование бесконечно-удаленной части плоскости 2.3 Построение качественной картины поведения траектории в круге Пуанкаре Заключение Список использованных источниковПриложение. Поведение траекторий системы (2.1) Введение Известно, что аналитический вид решения очень хорош в случае линейных систем. В случае же нелинейных систем даже тогда, когда решение может быть выражено через элементарные функции, эти выражения могут быть столь сложными, что непосредственный их анализ практически невозможен. В связи с этим появилась необходимость в создании такой теории, с помощью которой можно было бы изучать свойства решений дифференциальных уравнений по виду самих уравнений. Такой теорией, наряду с аналитической, и является качественная теория дифференциальных уравнений. Впервые задача качественного исследования для простейшего случая системы двух дифференциальных уравнений
с полной отчетливостью была поставлена А. Пуанкаре [7] в конце прошлого столетия. Позднее исследования А. Пуанкаре были дополнены И. Бендиксоном [3,с.191-211] и уточнены Дж. Д. Биркгофом [4,с. 175-179]. Одной из задач качественной теории дифференциальных уравнений является изучение поведения траекторий динамической системы (0.1) на фазовой плоскости в целом в случае, когда P(x,y) и Q(x,y) – аналитические функции. Интерес к изучению этой системы или соответствующего ей уравнения объясняется их непосредственным практическим применением в различных областях физики и техники.
Н.Н. Баутиным [1, с. 181- 196] и Н. Н. Серебряковой [8, с. 160- 166] полностью исследован характер поведения траекторий системы (0.1), имеющей два алгебраических интеграла в виде прямых. В [10, с. 732- 735] Л. А. Черкасом такое исследование проведено для уравнения (0.2) при наличии частного интеграла в виде кривой третьего порядка. Яблонский А. И. [11, с. 1752- 1760] и Филипцов В. Ф. [9, с. 469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. Рассмотрим систему дифференциальных уравнений
В настоящей работе проводится качественное исследование в целом системы (0.3) при условии, что она имеет два частных интеграла вида: x3+a1x2y+b1xy2+g1y3+a2x2+b2xy+g2y2+b3x+g3y+d=0, (0.4) mx+ny+p=0 (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя соотношениями. Во второй главе проводится качественное исследование системы, включающее в себя нахождение и исследование состояний равновесия, исследование бесконечно-удаленной части плоскости при фиксированных значениях коэффициентов системы. 1 ПОСТРОЕНИЕ КВАДРАТИЧНЫХ ДВУМЕРНЫХ СТАЦИОНАРНЫХ СИСТЕМ1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой третьего порядкаРассмотрим систему дифференциальных уравнений
Согласно [10, с. 1752-1760], если система, правые части которой есть полиномы n-ой степени, имеет частный интеграл вида:
где Fk(x,y) – однородные полиномы от x и y степени k, то выполняется равенство:
Пусть частный интеграл (1.2) имеет вид: F(x,y)ºx3+a1x2y+b1xy2+g1y3+a2x2+b2xy+g2y2+b3x+g3y+d=0 (1.4) Для интеграла (1.4) системы (1.1) имеет место соотношение (1.3),где L(x,y) = fx+gy+k, f, g, k – постоянные: (3x2+2a1xy+b1y2+2a2x+b2y+b3)(ax+by+a1x2+2b1xy+c1y2)+(a1x2+ 2b1xy+3g1y2+b2x+2g2y+g3)(cx+dy+a2x2+2b2xy+c2y2)=(x3+a1x2y+b1xy2+ (1.5) g1y3+a2x2+b2xy+g2y2+b3x+g3y+d)(fx+gy+k). Приравнивая в (1.5) коэффициенты при одинаковых степенях выражений xm yn слева и справа, получим следующую связь между коэффициентами кривой (1.4) и системы (1.1): 3a1+a1a2-f=0, (1.61) (2a1+2b2-f)a1+2a2b1-g+6b1=0, (1.62) 2a1c1+(2b1+2c2-g)b1+(6b2-f)g1=0, (1.63) (4b1+c2-g)a1+(a1+4b2-f)b1+3a2g1+3c1=0, (1.64) c1b1+(3c2-g)g1=0; (1.65) ca1+(2a1-f)a2+a2b2-k+3a=0, (1.71) (2a+d-k)a1+2cb1+(4b1-g)a2+(a1+2b2-f)b2+2a2g2+3b=0, (1.72) 2ba1+(a+2d-k)b1+3cg1+2c1a2+(2b1+c2-g)b2+(4b2-f)g2=0, (1.73) bb1+(3d-k)g1+c1b2+(2c2-g)g2=0; (1.74) (2a-k)a2+cb2+(a1-f)b3+a2g3=0, (1.81) 2ba2+(a+d-k)b2+2cg2+(2b1-g)b3+(2b2-f)g3=0, (1.82) bb2+(2d-k)g2+c1b3+(c2-g)g3=0; (1.83) (a-k)b3+cg3-df=0, (1.91) bb3+(d-k)g3-dg=0, (1.92) dk=0. (1.93) Будем предполагать, что коэффициенты кривой (1.4) и системы (1.1) вещественные и кривая не проходит через начало координат, тогда d=0. Согласно (1.93) в этом случае k=0. Будем рассматривать частный случай системы (1.1), т.е. будем предполагать, что a2=c1=0, а коэффициенты a1, b1, g1 интегральной кривой (1.4) обращаются в нуль. Уравнения (1.61) – (1.93) при этих предположениях будут иметь вид: 3a1-f=0, (1.101) g+6b1=0; (1.102) (2a1-f)a2+3a=0, (1.111) (4b1-g)a2+(a1+2b2-f)b2+3b=0, (1.112) (2b1+c2-g)b2+(4b2-f)g2=0, (1.113) (2c2-g)g2=0; (1.114) 2aa2+cb2+(a1-f)b3=0, (1.121) 2ba2+(a+d)b2+2cg2+(2b1-g)b3+(2b2-f)g3=0, (1.122) bb2+2dg2+(c2-g)g3=0; (1.123) ab3+cg3-df=0, (1.131) bb3+dg3-dg=0. (1.132) Из условий (1.101) и (1.102) получаем, что f = 2a1, g = 6b1. Из условия (1.114) имеем (2c2-g)g2=0. Пусть g2 2c2-g=0 и g=2c2, с другой стороны g = 6b1, значит c2=3b1. Имея условия f = 2a1, g = 6b1, c2=3b1, из соотношений (1.111) – (1.113), (1.121), (1.123) и (1.131) найдем выражения коэффициентов кривой (1.4) через коэффициенты системы(1.1) в следующем виде: a2 = g2 = g3 = d = Равенства (1.122) и (1.132) с учетом полученных выражений (1.15), дадут два условия, связывающие коэффициенты a, b, c, d, a1, b1, b2: (2ab1-ba1)[3(32a1b1b2-15a12b1-16b1b22) a+(8a1b22-18a12b2+9a13) b+ 24(a1b12-b12b2) c+(16a1b1b2-15a12b1) d]=0, (1.16) (2ab1-ba1)[12(7a1b1b2-3a12b1-4b1b22) a2+6(3a1b12-4b12b2) ac+(3a12b1- -4a1b1b2) bc+2(4a12b2-3a13)bd –8a1b12cd+4a12b1d2]=0. (1.17) Итак, установлена следующая теорема: Теорема 1.1 Система (1.1) имеет частный интеграл вида (1.4), коэффициенты которого выражаются формулами (1.15), при условии, что коэффициенты системы связаны соотношениями (1.16), (1.17) и c1=a2= 0, c2= 3b1. 1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой первого порядкаРассмотрим система (1.1), которая в качестве частного интеграла (1.2) имеет кривую первого порядка: mx+ny+p=0. (1.18) В системе (1.1), согласно предыдущего параграфа a2=c1=0, c2=3b1. (1.19) Для интеграла (1.18) системы (1.1), с учетом (1.19), имеет место соотношение (1.3), где L(x,y)= ax+by+g, a, b, g – постоянные: m(ax+by+a1x2+2b1xy)+n(cx+dy+2b2xy+3b1y2)= =(mx+ny+p)( ax+by+g). (1.20) Приравнивая в (1.20) коэффициенты при одинаковых степенях xm yn, получим следующую связь между коэффициентами кривой (1.18) и системы (1.1): (a1-a)m= 0, (1.211) (2b1-b)m+(2b2-a)n=0, (1.212) (3b1-b)n=0; (1.213) (a-g)m+cn-pa=0, (1.221) bm+(d-g)n-bp= 0, (1.222) pg= 0. (1.223) Предположим, что кривая не проходит через начало координат, то есть p¹0. Тогда из условия (1.223) получаем, что g=0. Условия (1.221), (1.222) запишутся в виде: am+cn-pa=0, (1.231) bm+dn-bp= 0. (1.232) Из условий (1.211) и (1.213) имеем: (a1-a)m= 0, (3b1-b)n=0. Пусть m¹0, тогда a1-a=0 и a=a1, (1.24) а при n¹0, получаем, что 3b1-b=0 и b=3b1. (1.25) Учитывая (1.24) и (1.25) из условия (1.212) находим выражение коэффициента m: m= а соотношение (1.231) даст значение коэффициента p: p= Из равенства (1.232), с учетом полученных выражений (1.26) и (1.27), находим условие на коэффициенты системы (1.1): [3(a1b1-2b1b2) a+(2a1b2-a12) b-3b12c+a1b1d] n=0. (1.28) Итак, установлена следующая теорема: Теорема 1.2 Система (1.1) имеет частный интеграл (1.18), коэффициенты которого выражаются формулами (1.26),(1.27), при условии, что коэффициенты системы связаны соотношением (1.28) и c1=a2= 0, c2= 3b1. 1.3 Необходимые и достаточные условия существования у системы (1.1) двух частных интегралов (1.4), (1.18)В разделах 1, 2 мы получили, что система (1.1) будет иметь два частных интеграла в виде кривых третьего и первого порядков при условии, что коэффициенты системы связаны соотношениями: (2ab1-ba1)[3(32a1b1b2-15a12b1-16b1b22) a+(8a1b22-18a12b2+9a13) b+ 24(a1b12-b12b2) c+(16a1b1b2-15a12b1) d]=0, (2ab1-ba1)[12(7a1b1b2-3a12b1-4b1b22) a2+6(3a1b12-4b12b2) ac+(3a12b1- -4a1b1b2) bc+2(4a12b2-3a13)bd –8a1b12cd+4a12b1d2]=0, [3(a1b1-2b1b2) a+(2a1b2-a12) b-3b12c+a1b1d] n=0. Причем b1¹0, a1¹0, 2b1a-ba1¹0. Рассмотрим частный случай, т.е. будем предполагать, что коэффициенты a1= Следовательно, наши соотношения запишутся в виде:
- - Выразим из условия (1.30) коэффициент c c= подставим (1.33) в равенство (1.31), найдем коэффициент d d= Из условия (1.32), учитывая (1.33) и (1.34) находим b= Получаем, что коэффициенты системы (1.1) определяются по следующим формулам: b= c=- d=- a1= Равенства (1.15), (1.26) и (1.27), при условии, что имеют место формулы (1.35), дадут следующие выражения для коэффициентов интегралов (1.4) и (1.18): a2=12a, b2= - g2=a, b3= g3= - m= - Теорема 1.3 Система (1.1) имеет два частных интеграла вида (1.4) и (1.18) с коэффициентами, определенными формулами (1.36), при условии, что коэффициенты системы (1.1) выражаются через параметры по формулам (1.35). 2 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ТРАЕКТОРИЙ СИСТЕМЫ НА ПЛОСКОСТИ 2.1 Исследование системы (1.1) с коэффициентами, заданными формулами (1.35) в конечной плоскостиПусть мы имеем систему (1.1), коэффициенты которой определяются согласно формулам (1.35),т.е. систему:
Интегральные кривые (1.4),(1.18), согласно формулам (1.36), имеют вид: x3+12ax2- - Найдем состояния равновесия системы (2.1). Приравняв правые части системы к нулю и исключив переменную x, получим следующее уравнение для определения ординат состояний равновесия: 8192y4-11776ay3+5480a2y2-825a3y=0. (2.4) Из (2.4) получаем, что y0=0, y1= Абсциссы точек покоя имеют вид: x0=0, x1= - Согласно (2.5) и (2.6)
заключаем, что система (2.1) имеет четыре состояния равновесия - Исследуем поведение
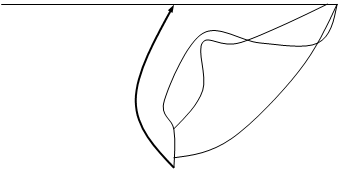
траекторий в окрестностях состояний равновесия 1. Исследуем точку Составим
характеристическое уравнение в точке
Отсюда
Следовательно, характеристическое уравнение примет вид:
Характеристическими
числами для точки
Корни 2. Исследуем точку Составим характеристическое уравнение в точке A. Согласно равенствам (2.7) характеристическое уравнение примет вид:
то есть
Корни 3. Исследуем точку Применяя равенства (2.7), составим характеристическое уравнение в точке B:
Корни 4. Исследуем точку Учитывая выражения (2.7), составим характеристическое уравнение в точке:
Характеристическими
числами для точки
Корни 2.2 Исследование бесконечно-удаленной части плоскости Очень важным для исследования вопроса о наличии замкнутых траекторий являются сведения о поведении траекторий при удалении в бесконечность, то есть исследование бесконечно-удаленных частей плоскости. Для этого воспользуемся преобразованием Пуанкаре [7]:
которое позволяет изучить особые точки лежащие на экваторе сферы Пуанкаре вне концов оси OY. Имеем
Значит преобразование (2.8) переводит систему (1.1) в систему:
Введем новое время
Изучим бесконечно-удаленные точки на оси u, т.е. при z=0. Получаем
Приравнивая второе уравнение системы (2.11) к нулю, получаем
Таким образом, состоянием
равновесия являются две точки N1(0,0) N2(0, Исследуем характер точек N1, N2. 1. Исследуем точку N1(0,0). Составим характеристическое уравнение системы (2.10) в точке N1:
Согласно выражениям (2.12), получаем характеристическое уравнение:
Получим, что
Корни 2. Исследуем точку N2(0, Учитывая выражение (2.12), составим характеристическое уравнение в точке N2:
соответственно характеристическими числами будут являться
Корни Исследуем бесконечно-удаленную часть плоскости в конце оси OY с помощью преобразования [7]
Это преобразование систему (2.1) переводит в систему:
Введем новое время
При z=0, получаем:
Приравнивая второе уравнение системы (2.16) к нулю, получаем
Для исследования состояний равновесий на концах оси OY, необходимо исследовать только точку N3(0,0). Составим характеристическое уравнение системы (2.16) в точке N3:
соответственно характеристическими числами будут являться
Корни Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 1. Таблица 1.
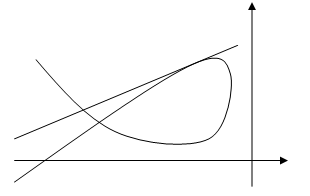
Примечание: через с, у+, у- обозначены соответственно седло, устойчивый узел, неустойчивый узел. Положение кривых (1.4), (1.18) и расположение относительно их состояний равновесия при a>0 и a<0 дается соответственно рис. 1(а,б).
а) (a>0)
б) (a<0) Рис.1 2.3 Построение качественной картины поведения траектории в круге Пуанкаре Поскольку три состояния равновесия A, B, C расположены на интегральных кривых, то вопроса существования предельных циклов вокруг этих точек не возникает. Начало координат расположено вне интегральных кривых и является седлом с индексом (-1). Предельные циклы могут окружать состояния равновесия с индексом (+1). Отсюда заключаем, что изучаемая система предельных циклов не имеет. Поведение сепаратрис седла O, B легко выяснить. Сепаратрисы седла В полностью определяются интегральными кривыми. Сепаратрисы седла О(0,0) однозначно выясняются с помощью изучения поля направления системы на осях координат. Так для а>0 α – сепаратрисы седла О примыкают к точке С и N3, а ω – сепаратрисы примыкают к точке А и N1, а при а<0 a-сепаратрисы примыкают к точке А и N1, w - сепаратрисы – к точке С и N3. В результате получаем, что качественная картина исследования траекторий в целом при а>0 определяется рисунком 2а приложения, а при а<0 – рисунком 2б приложения. ЗАКЛЮЧЕНИЕ В данной дипломной работе построена квадратичная двумерная стационарная система, имеющая два частных интеграла в виде кривых третьего и первого порядков. При этом коэффициенты кривых выражаются через произвольный параметр системы. Проведено качественное исследование полученной системы, найдены четыре состояния равновесия, три из которых А, В, С принадлежат интегральным кривым. Исследована бесконечно-удаленная часть плоскости, доказано отсутствия предельных циклов, выяснено поведение сепаратрис седел и построена качественная картина поведения траекторий системы в целом. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ1 Баутин Н.Н. О числе предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра // Матем. сб.- 1952.- Т.30,№1.- 458 с. 2 Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости.-М.: Наука, 1976.- 274 с. 3 Бендиксон И. О кривых, определяемых дифференциальными уравнениями.- УМН, 1941.- Вып. 9.- 643 с. 4 Биркгоф Дж.Д. Динамические системы. М.-Л.: Гостехиздат, 1941.- 340 с. 5 Воробьев А.П. К вопросу о циклах вокруг особой точки типа “узел” // ДАН БССР.- 1960.- Т.4,№9.- 720 с. 6 Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую.- ПММ.- 1952.- Т.16, Вып. 6.- с.659-670. 7 Пуанкаре А. О кривых, определяемых дифференциальными уравнениями.- М.-Л.: ГИТТЛ, 1947.- 839 с. 8 Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний.- ПММ.- 1963 Т.27, Вып.1.- 230 с. 9 Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения.- 1973.- Т.9,№3.- 256 10
Черкас
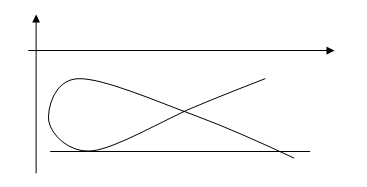
Л.А. Об алгебраических решениях уравнения 11 Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения.- 1970.- Т.6,№10.- с. 1752-1760. ПРИЛОЖЕНИЕПоведение траекторий системы (2.1)
а) (а>0)
б) (а<0)Рис. 2 |
|||||||||||||||||||||||||||||||||||||||
 Реферат
Реферат Содержание
Содержание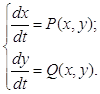 (0.1)
(0.1)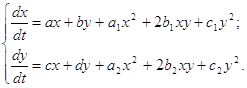 (0.3)
(0.3)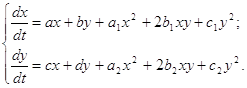 (1.1)
(1.1)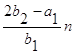 , (1.26)
, (1.26)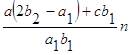 . (1.27)
. (1.27) 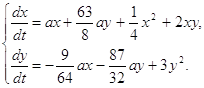 (2.1)
(2.1)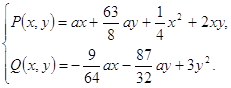
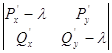 =
=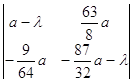 =0.
=0.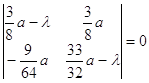
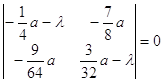
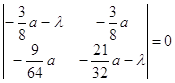
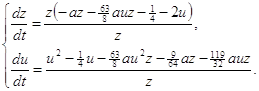 (2.9)
(2.9) 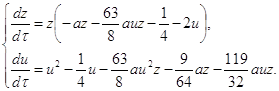 (2.10)
(2.10)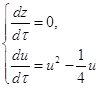 (2.11)
(2.11)
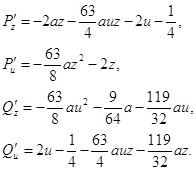 (2.12)
(2.12)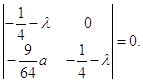
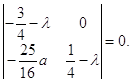
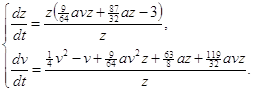 (2.14)
(2.14)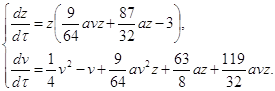 (2.15)
(2.15)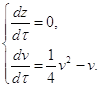 (2.16)
(2.16)