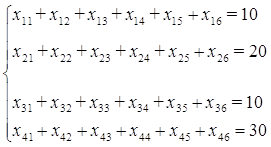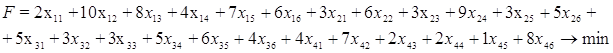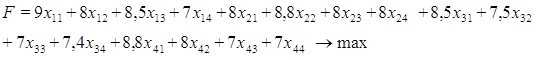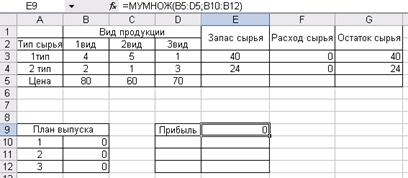
Контрольная работа: Анализ экономических задач оптимизации

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

Волгоградский филиал

Кафедра высшей математики и информатики

Контрольная работа

по дисциплине: Информационные технологии в торговле

Исполнитель: студент 4 курса заочной формы обучения

факультета: «Экономика и управление на предприятии (торговли)»

Каплунова Ольга Александровна

Рецензент: Дмитриева Ирина Сергеевна

Волгоград 2008г.

СОДЕРЖАНИЕ

Задача №1 Производственная задача №3

Задача №2 Оптимальная организация рекламной компании №7

Задача №3 Транспортная задача №8

Задача №4 Задача об оптимальном назначении№8

Задача №1 Производственная задача

Постановка задачи.

При производстве трех видов продукции используют два типа сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные таковы:

Таблица 1.1

Запас сырья	Расход сырья на единицу продукции
Запас сырья	№1	№2	№3
40	4	5	1
24	2	1	3
Прибыль в у.е.	80	60	70

Экономико-математическая модель.

Обозначим за (i =1….3) объем производства соответствующей продукции.

С учетом значений задачи получаем.

4х1 + 5х2 + 1х3 ≤ 40

2х1 + 1х2 + 3х3 ≤ 24

Дополнительные ограничения:

, , .

Необходимо найти оптимальный план выпуска продукций (т.е. ), который обеспечит максимальную выручку.

Исходя из условий задачи целевая функция принимает вид:

Табличная модель.

Рис. 1.1. Табличное представление модели

Более наглядно заполнение ячеек табличной формы задачи представлено на рисунке 1.2.

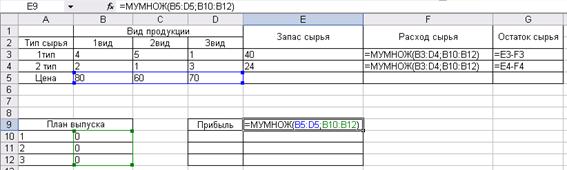
Рис. 1.2. Табличная модель с представленными формулами

Оптимизация. Сервис Поиск решений.

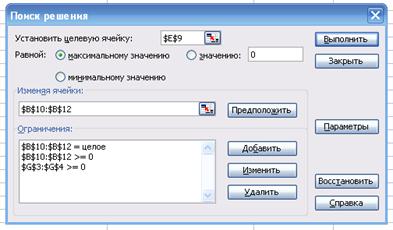
Рис. 1.3. Диалоговое окно надстройки Поиск решения

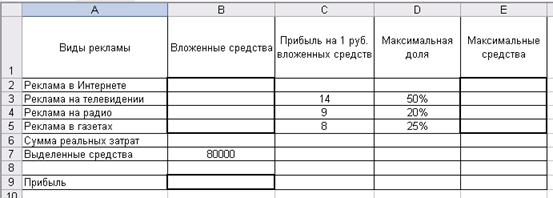
Рис. 1.4. Решение производственной задачи

Вывод: Оптимальный план производства, при данных условиях, состоит в том, что продукцию 1-ого и 3-ого видов необходимо производить в объеме 9 и 2 ед. соответственно, а продукции 2-ого вида не выпускать в производство. При этом обеспечивается максимальная выручка в размере 860 д.е.

Задача №2 Оптимальная организация рекламной компании

Постановка задачи.

На рекламу выделено 80000 руб. Предприятие рекламирует свою деятельность, используя четыре источника массовой информации: Интернет, телевидение, радио, газеты. Анализ рекламной деятельности в прошлом показал, что вложенные в рекламу средства приводят к увеличению прибыли на 16, 14, 9, 8 руб соответственно, в расчете на 1 руб, затраченный на рекламу. Руководство намерено потратить половину суммы на рекламу на телевидении, не менее 20% выделенной суммы - на радио, не более 25% - на газеты. Определить оптимальное распределение средств, направляемых на рекламу.

Экономико-математическая модель.

– средства, направленные на Интернет;

– средства, направленные на телевидение;

– средства, направленные на радио;

– средства, направленные на газеты.

Целевая функция:

Ограничения:

х1 + х2 + х3 + х4 = 80000,

х2 ≤ 0,5 * 80000,

х3 ≥ 0,2 * 80000

х4 ≤ 0,25 * 80000

х1 ≥ 0, х2 ≥ 0, х3 ≥ 0, х4 ≥ 0.

Табличная модель.

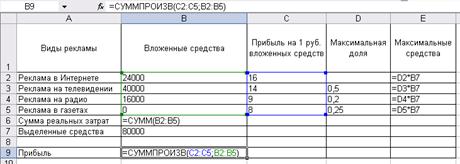
Рис. 2.1 Табличное представление модели

Рис. 2.2 Табличная модель с представленными формулами

Оптимизация. Сервис Поиск решения.

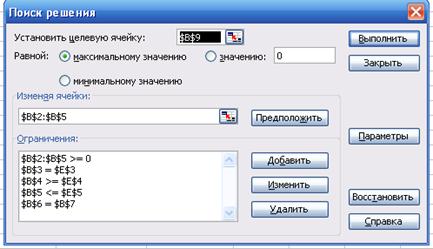
Рис. 2.3 Диалоговое окно надстройки Поиск решения

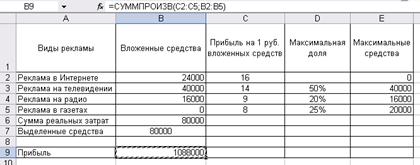
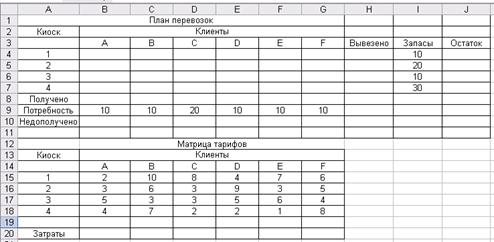
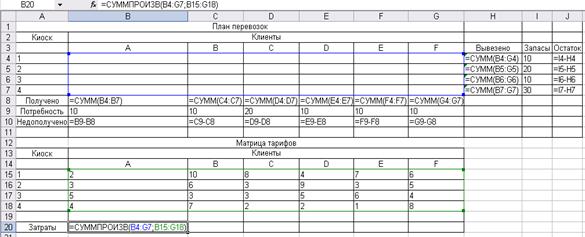
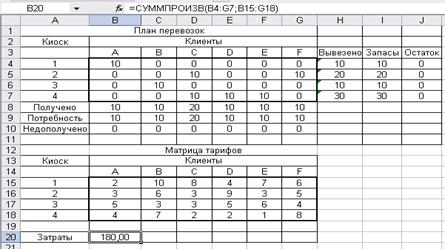
Рис. 2.4 Решение задачи об оптимальной организации рекламной компании

Вывод: Для получения максимальной прибыли, предприятие, проводя рекламную компанию, должно вложить 24000 руб. на рекламу – в Интернете, 40000 руб. в рекламу на телевидении, 16000 р. – в рекламу на радио, и не вкладывать средства на рекламу в газетах. При этом максимальная прибыль составит 1088000 руб.

Задача №3 Транспортная задача

Постановка задачи.

Фирма по доставке букетов цветов имеет шесть постоянных клиентов. Цветы поставляются из четырех киосков, где ежедневный запас составляет: 10, 20, 10, 30 букетов соответственно. Фирма получила заказ от постоянных клиентов: А, В, D, E, F по 10 букетов, C – 20 букетов. Удельные затраты на поставку букетов от каждого киоска каждому клиенту представлены в таблице. Определить объем поставки из каждого киоска каждому клиенту так, чтобы минимизировать суммарные затраты.

Киоск	Клиенты
Киоск	А	В	С	D	E	F
1	2	10	8	4	7	6
2	3	6	3	9	3	5
3	5	3	3	5	6	4
4	4	7	2	2	1	8

Экономико-математическая модель.

Искомый объем перевозки от i-ого поставщика к j-ому потребителю обозначим через . Тогда определяются ограничения для условия реализации всех мощностей:

Ограничения для удовлетворения спросов всех потребителей:

х11 + х21 + х31 + х41 = 10

х12 + х22 + х3 2+ х42 = 10

х13 + х23+ х33 + х43 = 20

х14 + х24 + х34 +х44 = 10

х15 + х25 + х35 + х45 = 10

х16 + х26 +х36 + х16 = 10

Суммарные затраты на перевозку выражаются через коэффициенты затрат и поставки и определяют целевую функцию.

Табличная модель.

Рис. 3.1.Табличное представление модели

Рис. 3.2. Табличная модель с представленными формулами

Оптимизация. Сервис Поиск решения.

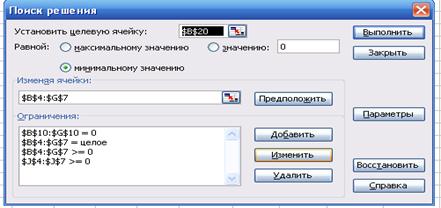
Рис. 3.3. Диалоговое окно надстройки Поиск решения

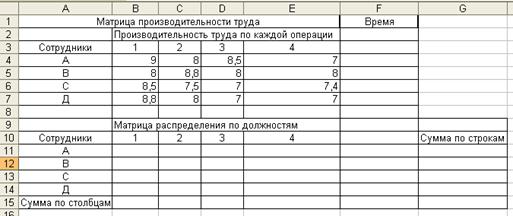
Рис. 3.4. Решение транспортной задачи

Вывод: Минимальные суммарные затраты на доставку букетов цветов в размере 180 д.е. достигаются путем распределения поставок, представленных в ячейках [B4:G4]и[B6:G6] . Так, например, киоск 2 должен доставить клиенту C 10 ед. букетов и клиенту F 10ед. букетов. К клиентам A, В, D, E ехать не надо. А киоск 4 должен доставить клиентам C, D, E, по 10 ед. букетов. А к клиентам A, B, F ехать не надо.

Задача №4 Задача об оптимальном назначении

Постановка задачи.

На упаковочной поточной линии работают четыре сотрудника. Операции упаковки последовательны. Время работы (в мин.) каждого сотрудника на каждой операции представлено в таблице. Необходимо наладить процесс упаковки так, чтобы сократить общее время упаковки (повысить производительность).

Операции	Сотрудники
Операции	А	В	С	D
1	9	8	8,5	7
2	8	8,8	8	8
3	8,5	7,5	7	7,4
4	8,8	8	7	7

Экономико-математическая модель. Данная задача является типичной моделью линейного целочисленного программирования (Ц.Л.П.), так как включает в себя двойственные ограничения на переменные (1- сотрудник назначается на должность, 0- сотрудник не назначается на должность).

– сотрудник A назначается на должность № 1;

– сотрудник A назначается на должность № 2;

х13 - сотрудник A назначается на должность № 3;

– сотрудник A назначается на должность № 4;

– сотрудник B назначается на должность № 1;

– сотрудник B назначается на должность № 2;

х23 - сотрудник B назначается на должность № 3;

– сотрудник B назначается на должность № 4;

– сотрудник C назначается на должность № 1;

– сотрудник C назначается на должность № 2;

х33 - сотрудник C назначается на должность № 3;

– сотрудник C назначается на должность № 4;

х 41– сотрудник D назначается на должность № 1;

– сотрудник D назначается на должность № 2;

х43 - сотрудник D назначается на должность № 3;

– сотрудник D назначается на должность № 4;

Имеем матрицу переменных:

х11 х12 х13 х14

х21 х22 х23 х24

х31 х32 х33 х34

х41 х42 х43 х44

Целевая функция выражает суммарную производительность и имеет вид:

Ограничения:

Матрица переменных принимает двоичное значение:

1- сотрудник назначается на должность;

0- сотрудник не назначается на должность.

Табличная модель.

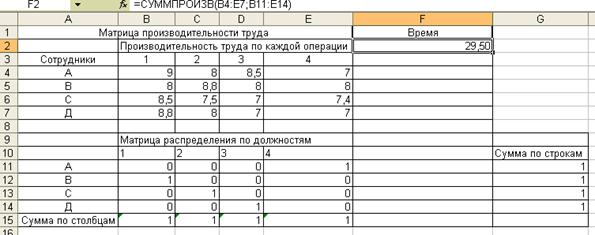
Рис. 4.1. Табличное представление модели

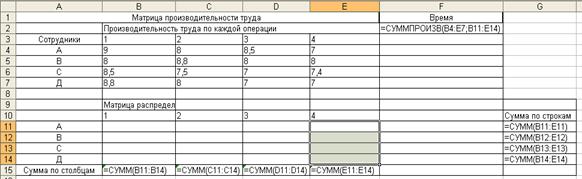
Рис. 4.2. Табличная модель с представленными формулами

Оптимизация. Сервис Поиск решения.

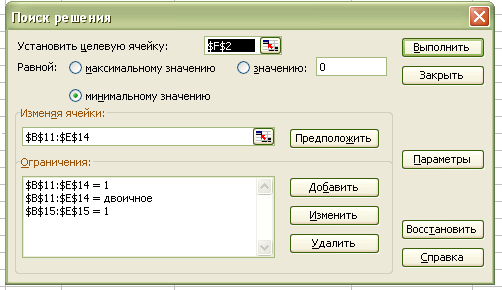
Рис. 4.3Диалоговое окно надстройки Поиск решения

Рис. 4.4. Решение задачи об оптимальном назначении

Вывод: С учетом производительности труда всех работников по каждой операции, менеджеру необходимо назначить: сотрудника A на должность № 4, сотрудника B на должность №1, сотрудника C на должность №2, сотрудника D на должность №3,. При этом коллектив добьется общей времени упаковки 29,50 мин.