- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
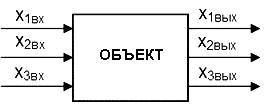
Контрольная работа: Идентификация объекта управленияКонтрольная работа: Идентификация объекта управленияИдентификация объекта управленияВ современных сложных объектах, как правило, выходной сигнал объекта зависит не от одного входного сигнала, как в случае с кривой разгона, а от нескольких входных сигналов, т.е. объект управления имеет сложное переплетение взаимосвязей входных и выходных сигналов.
Рис. 1. Схема объекта, состоящего из нескольких взаимосвязанных входных-выходных сигналов Для идентификации таких сложных объектов используется метод регрессионного анализа с проведением активного эксперимента на базе теории математического планирования эксперимента. Назначение этой теории – значительно сократить количество экспериментальных опытов и упростить расчеты, необходимые для получения уравнения взаимосвязи выходного сигнала с несколькими входными сигналами – уравнения регрессии. Сокращение числа необходимых
экспериментов в теории математического планирования эксперимента достигается за
счет одновременного изменения всех входных сигналов (факторов), а упрощение
расчетов получается за счет того, что изменение входных сигналов (факторов)
нормируется, т.е. величины
Рис. 2. Схема исследования объекта методом регрессионного анализа для двух входных сигналов (факторов) Точка О – номинальный режим работы
объекта. Нормализация происходит за счет того, что начало координат переносится
в точку О на
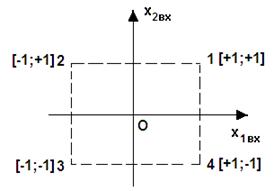
Рис. 3. Схема центрального плана полного факторного эксперимента для двух входных сигналов (факторов) Здесь (рис. 3) изображен план
проведения опытов для изучения зависимости На приведенном выше рис. 3. изображен центральный (точка О – в центре) ортогональный полный факторный план эксперимента для 2-х входных факторов. Таблица 1. Полный факторный эксперимент для k=2.
Свойство плана, когда, называется ортогональностью плана. Таблица 2. Полный факторный эксперимент для k=3.
В полном факторном плане экспериментов число опытов резко возрастает в зависимости от числа входных факторов: k=4 N=16; k=5, N=32; k=6, N=64 опыта. Поэтому для сокращения числа опытов с минимальной потерей информации применяются сокращенные планы – дробные реплики. Если планы содержат половину опытов полного факторного эксперимента, то такой план носит название полуреплики. Таблица 3. Пример полуреплики для k=4 (ПФЭ=16)
Используют также ¼ реплики от полного факторного эксперимента. Уравнение взаимосвязи входного и выходного сигналов – уравнение регрессии – записывается в виде алгебраического полинома 1-ой и 2-ой степени в следующем виде: 1-ой степени: xвых = b0 +b1x1+b2x2; с учетом взаимодействия входных факторов для 2-х входных факторов x1 и x2: xвых = b0 + b1x1 + b2x2 + b12x1 x2 . Полином второй степени – уравнение регрессии:
Естественно, это уравнение более точно описывает взаимосвязь xвых – функции отклика – с входными факторами (сигналами) объекта. Задача идентификации объекта управления (ОУ) методом регрессивного анализа сводится к выбору порядка математической модели – уравнения регрессии – и определению коэффициентов b0, b1, b2, b12 и т.д. в этом уравнении регрессии. При определении этих коэффициентов используется метод наименьших квадратов, в котором определяется наименьшая сумма отклонений в квадрате (2-ой степени) между реально полученным в эксперименте выходным сигналом и выходным сигналом, рассчитанным (предсказанным) по уравнению регрессии, т.е. ищут минимум функции:
Минимум функции Ф достигается в том случае, когда первая частная производная (тангенс угла наклона к впадине) равна нулю, т.е.
Пример
Рассмотрим пример использования
метода наименьших квадратов. Пусть выходной сигнал (функция отклика) зависит от
одного фактора (входного сигнала). Активно проведено n экспериментов. Задана xвых = b0 + b1x1 Методом наименьших квадратов ищем минимум функции Ф:
Для получения минимума этой Ф приравниваем к нулю частные производные
Для удобства получения частных производных введем фиктивную переменную x0=1 и функцию Ф запишем:
x0=1 можно убрать. Тогда
Решая эту систему алгебраических уравнений (можно методом Крамера), находим:
Проверка идентичности математической модели – уравнения регрессии исследуемого объекта проводится по нескольким критериям адекватности и идентичности модели. Поскольку результаты опытов в эксперименте заранее точно предсказать невозможно, то обработка и сами результаты связаны с неопределенностью или вероятностью. Вероятность изменяется в пределах: 0 – события быть не может, 1 – событие произойдет обязательно (день-ночь). При большом числе параллельных (одинаковые условия) опытов вероятность может быть задана в виде функции распределения вероятностей (рис. 4.):
Рис. 4. Схема нормального (гауссовского) закона распределения вероятностей На практике чаще всего используется так называемое нормальное (гауссовское) распределение вероятностей. Случайная величина ( Математическое ожидание – это среднее взвешенное значение случайной величины
Дисперсия характеризует разброс значений случайной величины относительно ее математического ожидания.
Проверка значимости уравнения
регрессии проводится по критерию Фишера или F-критерию. Проверка заключается в определении, значимо ли
(больше ошибки измерения) полученное уравнение
где f1 – число степеней свободы,
А также остаточную дисперсию:
f2 – число степеней свободы. Величину критерия Фишера (F-критерий) определяют по формуле:
Значимость коэффициентов bi уравнения регрессии определяют по t-критерию (критерии Стьюдента):
Идентификация объектов управления методом корреляционного анализаМетод корреляционного анализа используется для идентификации объектов управления в том случае, если входные и выходные сигналы являются случайными величинами.
Рис. 5. Схема исследования объекта корреляционным методом При корреляционном анализе используются: – автокорреляционная функция (АКФ) и – взаимокорреляционная функция (ВКФ). АКФ характеризует зависимость последующих значений случайной величины от предыдущих, находящихся на расстоянии Dt.
Рис. 6. График изменения входной случайной величины – входного сигнала АКФ:
При Dt ®0 – точнее. Взаимокорреляционная функция связывает две величины, отстоящие друг от друга на Dt. ВКФ:
С АКФ и ВКФ связаны (через преобразование Фурье, когда входной-выходной сигнал раскладывается в ряд Фурье, состоящий из суммы синусоидальных колебаний с различной w – ряд гармоник) спектральные плотности случайных величин.
Физически Через спектральную плотность находим АФЧХ объекта:
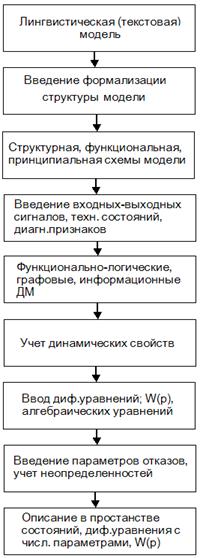
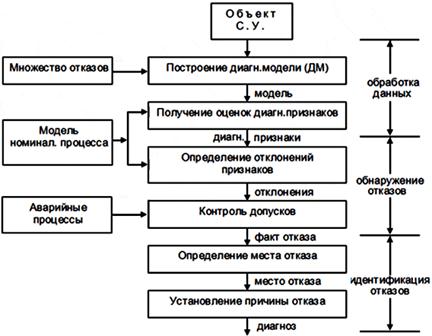
Техническая диагностика – наука о распознавании состояния технической системы. Диагнозис (гр.) – распознавание. Объект технического диагностирования – изделие и его составные части, техническое состояние которых подлежит определению с заданной точностью. Техническое состояние – совокупность свойств объекта, характеризуемая в данный момент времени признаками, установленными технической документацией на объект. Техническое состояние может быть: – исправное-неисправное; – работоспособное-неработоспособное; – функционирующее правильно и неправильно. Диагностирование по алгоритму – это совокупность предписаний с использованием диагностических признаков. Система технического диагностирования – совокупность средств и объекта диагностирования, а также и исполнителей, осуществляющих диагностирование по правилам, установленным соответствующей документацией. Система технической диагностики определяет состояние технического объекта, характер его изменения с течением времени, по определенным диагностическим признакам. Теоретический фундамент технической диагностики – теория распознавания образов, разработка алгоритмов распознавания, создание диагностических математических моделей, устанавливающих связь между состояниями технической системы и их отображением в пространстве диагностических признаков (сигналов). Диагнозы – классы типичных (типовых) состояний. Важная часть распознавания – правила принятия решений (решающие правила). Диагностика в режиме работы объекта называется функциональным техническим диагностированием. Диагностика, когда проводятся тестовые воздействия – тестовая техническая диагностика. В технической диагностике введено понятие глубины поиска дефекта, задаваемое указанием составной части объекта диагностики, с точностью, до которой определяется место дефекта. Обычно это модуль или блок, иногда даже микросхема (ЛОМИКОНТ). Актуальность технической диагностики подтверждается следующими цифрами: в США исследования показали техническое обслуживание и ремонт самолета в 3-4 раза больше его стоимости, ремонт и обслуживание радиотехнического оборудования – 1200% от его стоимости. В СССР (по 181 г.) ремонтом и обслуживанием металлорежущих станков занимались в 4 раза больше рабочих, чем изготовлением этого оборудования. Стоимость заводского ремонта в ВВС США в 187 г. составила 15 млрд. долл., что в 2 раза больше, чем в 180 г. Тенденция роста убытков, связанных с отказами техники, имеет место во всех развитых странах. Отказы, неисправности, поломки, сбои, ошибки и даже катастрофы – неизбежные факторы, дестабилизирующие процесс нормального функционирования объекта и системы управления. Имеется 3 причины отказов и катастроф: а) применение малоизученных физических явлений для создания изделий; б) несоблюдение принципа системности при проектировании изделий; применение несовершенных и неадекватных расчетных схем; в) "человеческий фактор" в разработке, производстве и эксплуатации изделий ("защита от дурака"). Так, например, недостаточная изученность свойств материалов и несовершенство расчетов привели к катастрофе в США реактивного пассажирского самолета "Комета", который развалился в воздухе. Причина – прямоугольные иллюминаторы, в углах которых возникла концентрация напряжений, что привело к разрушению корпуса самолета. Второй пример. В 167 г. во время наземных испытаний космического корабля "Аполлон" США возникло короткое замыкание в проводе под креслом космонавта – мгновенный пожар в избытке кислорода – погибли 3 человека. В США подсчитано в 156 г., что из-за ошибок рабочих и служащих возникло 2 млн. отказов промышленного оборудования, что стоило 2 млрд. долл. Причина большинства авиакатастроф – "человеческий фактор". Объективность "человеческого фактора" и необходимость его учета отражена в шуточных законах Мэрфи: 1. Инструмент падает туда, где может нанести наибольший вред. 2. Любая трубка при укорачивании оказывается слишком короткой. 3. После разборки и сборки какого-либо устройства несколько деталей оказываются лишними. 4. Количество имеющихся в наличии запчастей обратно пропорционально потребности в них. 5. Если какая-либо часть устройства может быть смонтирована неправильно, то всегда найдется кто-нибудь, кто так и сделает. 6. Все герметические стыки протекают. 7. При любом расчете число, правильность которого для всех очевидна, становится источником ошибок. 8. Необходимость внесения в конструкцию принципиальных изменений возрастает непрерывно по мере приближения к завершению проекта. Необходимость в разработке научно обоснованных методов технической диагностики и технических средств для реализации диагностических систем и комплексов подтверждают результаты исследований, по которым установлено, что специалист 25% времени тратит на определенные части изделия, где произошла неисправность, 62% – на определение неисправной детали и только 13% времени – на восстановление отказавшей детали. Техническое диагностирование использует технические математические модели. Отличие диагностических моделей от обычных математических моделей, которые отражают номинальный режим функционирования объекта или системы управления состоит в том, что диагностическая модель описывает существенные свойства аварийных режимов, вызванных различными отказами. Объект или система при разработке диагностической модели рассматриваются по следующей схеме (рис. 3.):
Рис. 7. Схема разработки диагностической модели объекта или системы управления Иерархия диагностических моделей (ДМ)
Рис. 8. Иерархия диагностических моделей Из схемы видно, что диагностические модели могут быть различной сложности: от простых описательных (текст) до математических моделей высокого уровня. Классификация отказова) по степени влияния: полные, частичные; б) по характеру проявления: окончательные, перемежающиеся; в) по степени связи: зависимые, независимые; г) по частоте проявления: однократные, многократные; д) по характеру возникновения: внезапные, постепенные; е) по математическим моделям: параметрические, сигнальные; ж) по видам проявления: обрывы, короткие замыкания, дрейф, переориентация, изменение эффективности. Задачи диагностирования по следующей схеме (рис. 9.):
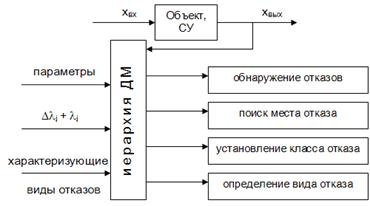
Рис. 9. Схема диагностирования по отказам Для диагностики моделей используется (см. классификацию) множество физических видов отказов – диагностических признаков. В качестве прямых диагностических признаков соответствующего отказа используют Dli = li - liном – отклонение диагностического параметра li от номинального значения. Косвенные диагностические признаки оценивают через отклонение величины xвых – выходного сигнала объекта (системы). Разработка диагностического обеспечения системы управления или объекта идет по следующей схеме (рис. 10.):
Рис. 10. Схема разработки диагностического обеспечения системы управления или объекта Математическая постановка задачи технического диагностирования объекта (системы управления)Пусть: а) задана система линейная с постоянными характеристиками на отдельном отрезке времени стационарная, работающая в номинальном режиме; б) задано множество контрольных точек; в) задано множество физических отказов с характеристикой отказов; г) задано множество тестовых и рабочих сигналов управления; д) задано время диагностирования ОУ (СУ). Требуется: Провести техническое диагностирование ОУ (СУ) в целях контроля технического состояния – обнаружение отказов, поиск места и определение причин отказа. При вероятностных методах
распознавания технического состояния системы вероятность постановки диагноза
Вероятность появления диагностического признака kj во всех состояниях объекта N независимо от их диагноза с учетом того, что kj появляется только в Nj состояниях объекта, равна:
Из изложенного выше вытекает, что вероятность совместного появления следующих событий: наличия у объекта диагноза Di и диагностического признака kj – равна:
Отсюда:
Формула Байеса неточно отражает реальное положение при постановке диагноза Di при наличии диагностического признака kj. Дело в том, что в этой формуле априорно (без доказательства, заранее) принято, что все диагностические признаки имеют равную вероятность появления в реальных условиях работы системы, при этом не учитывается информационная ценность того или иного диагностического признака. Информационная ценность диагностического признака определяется количеством информации, которое вносит данный диагностический признак в описание технического состояния объекта управления (ОУ) или системы управления (СУ). Количество информации связано с энтропией (степенью неопределенности) состояния системы, чем выше определенность состояния системы (меньше энтропия), тем меньше информации мы получим, изучая (диагностируя) эту систему (о ней и так почти все известно). Энтропия (степень неопределенности) системы по Шеннону (разработчик теории информации) находят по формуле:
где H(A) – энтропия системы A; P(Ai) – вероятность Ai состояния системы А. Количество информации определяется как разность энтропии системы в 2-х различных состояниях: J = H(A1) – H(A2), где J – количество информации, H(A1) – энтропия 1-го состояния, H(A2) – энтропия 2-го состояния системы. Список литературы1. Льюнг Леннарт. Идентификация систем. – М.: Наука, 191. 2. Интеллектуальные системы автоматического управления. / Под ред. И.М. Макарова, В.М. Лохина – М.: Физматпит, 2001. 3. В.О. Толкачев, Т.В. Ягодкина. Методы идентификации одномерных линейных динамических систем. – М.: МЭИ, 197. 4. К.А. Алексеев. Моделирование и идентификация элементов и систем автоматического управления. – Пенза, 2002. 5. Дочф Ричард, Вишоп Роберт. Современные системы управления. – М.: Юнимедиастайп, 2002. 6. С.В. Шелобанов. Моделирование и идентификация систем управления. – Хабаровск, 199. 7. К.В. Егоров. Основы теории автоматического регулирования. – М.: Энергия, 167. |
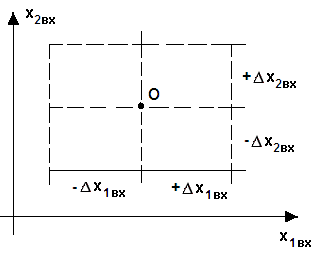
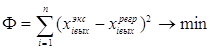
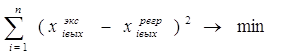
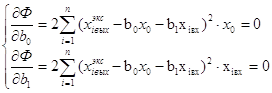
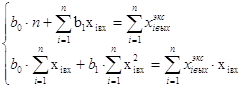
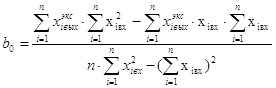
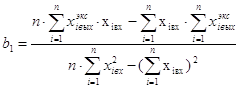
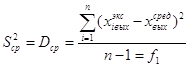 ,
,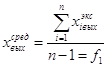 .
.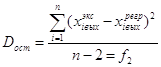 ,
,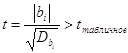 ,
,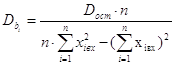 .
.
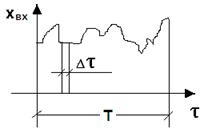
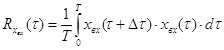 .
.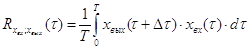 .
.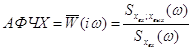 .
.
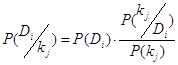 – формула Байеса.
– формула Байеса.