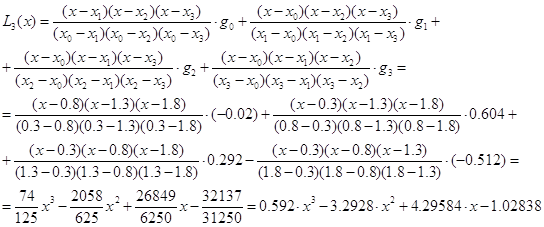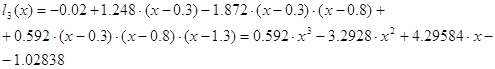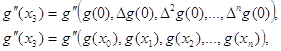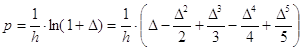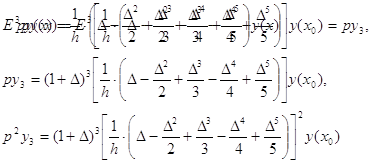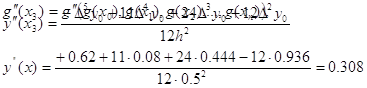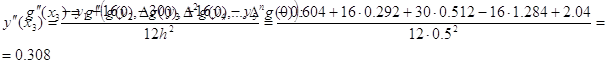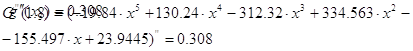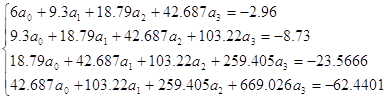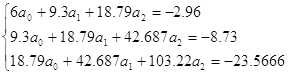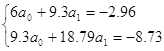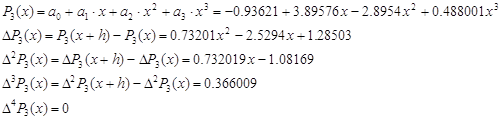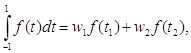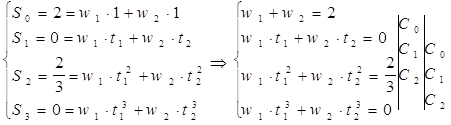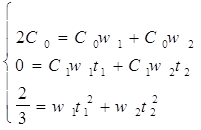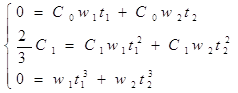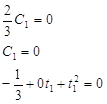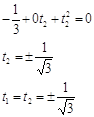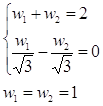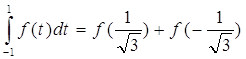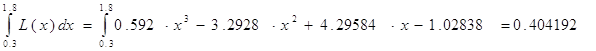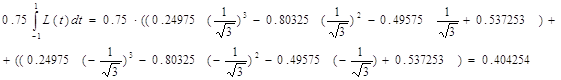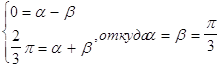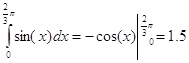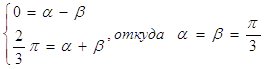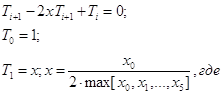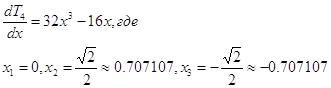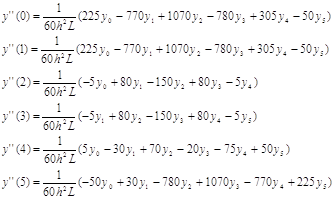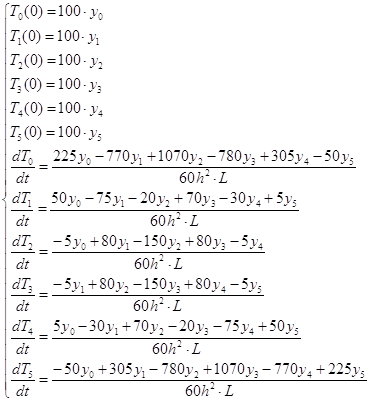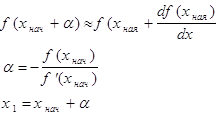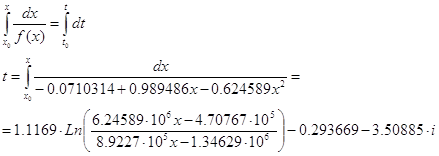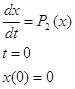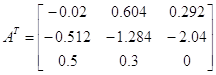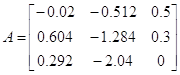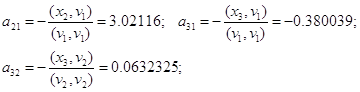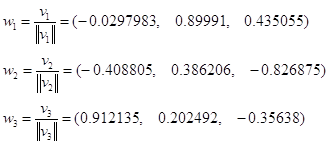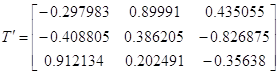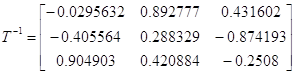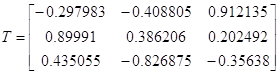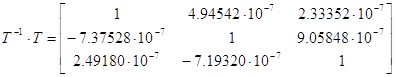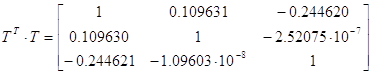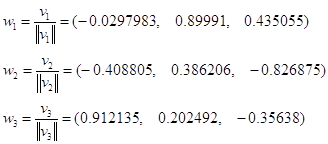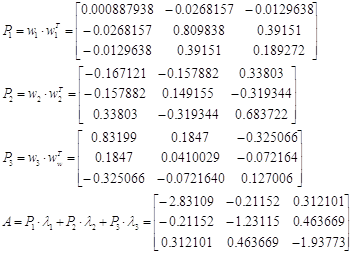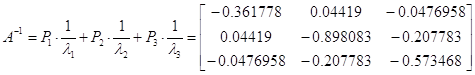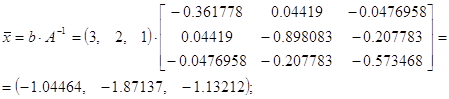Контрольная работа: Математический анализ
Контрольная работа: Математический анализ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
НАЦИОНАЛЬНЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ХПИ»
Кафедра
«Вычислительной техники и програмирования»
Расчётно–графическое задание
по курсу
«Теория алгоритмов и вычислительные методы»
Харьков –
2005
Исходные данные:
|
Вариант №
|
y0
|
y1
|
y2
|
y3
|
y4
|
y5
|
h
|
x0
|
| 64 |
-0.02 |
0.604 |
0.292 |
-0.512 |
-1.284 |
-2.04 |
0.5 |
0.3 |
Задача 1
Исходные данные вводятся
в ЭВМ как абсолютно точные числа и представляются в ней в виде чисел с
плавающей точкой с относительной погрешностью в одну миллионную. Введенные
данные x0 и y0 служат основой формирования двух векторов
x=(x0, x1, …, xn) и y=(y0, y1,
…, yn) по рекуррентным формулам:

Вычислить скалярное произведение с
:= (x, y) по алгоритму:
с := 0; i := 0;
while i
< n + 1 do c := c + xi · yi;
и оценить аналитически и
численно инструментальную абсолютную и относительную погрешности.
Решение
Поскольку данные
представляются в ЭВМ в виде чисел с плавающей точкой с относительной погрешностью,
то
x0 = x0(1+δ)
y0
= y0(1+δ)
C0
= x0y0(1+δ)
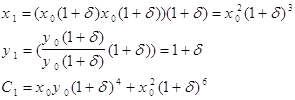
При
i = 1
При i = 2
x2
= x03(1+δ)5
y2
= y0(1+δ)3
C2
= x0y0(1+δ)5 + x02(1+δ)7
+ x03y0(1+δ)10
При i = 3
x3
= x04(1+δ)7
y3
= (1+δ)5
C3
= x0y0(1+δ)6 + x02(1+δ)8
+ x03y0(1+δ)11 + x04(1+δ)14
При i = 4
x4
= x05(1+δ)9
y4
= y0(1+δ)7
C4
= x0y0(1+δ)7 + x02(1+δ)9
+ x03y0(1+δ)12 + x04(1+δ)15
+ x05y0(1+δ)18
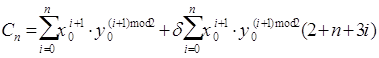
Выявим закономерность
изменения Ci:
При расчете Cn
без учета погрешности исходных данных и погрешности вычисления, получим
Обозначим эту сумму как S1.
Тогда абсолютная
погрешность S2
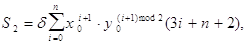
а относительная
погрешность
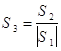
Оценим инструментально
относительную и абсолютные погрешности при n = 10
S1
= 0.0923071
S2
= 1.45914·10-6
S3
= 1.58075·10-5
Задача 2
Для функции g(x), заданной своими значениями в шести точках, составить
таблицу всех повторных разностей. Преобразовать функцию g(x) с помощью линейного преобразования x = a + b * k в функцию G(k) с целочисленным аргументом k. В качестве проверки правильности
заполнения таблицы вычислить аналитически конечную разность Δng(x) = ΔnG(k) для n = 5.
Решение
Составим таблицу всех
повторных разностей:
| k |
x |
y |
Δy |
Δ2y
|
Δ3y
|
Δ4y
|
Δ5y
|
| 0 |
0.3 |
0.02 |
-1.576 |
0.044 |
-0.136 |
0.66 |
-0.54 |
| 1 |
1.1 |
-1.556 |
-1.532 |
-0.092 |
0.524 |
0.12 |
— |
| 2 |
1.9 |
-3.088 |
-1.624 |
0.432 |
0.644 |
— |
— |
| 3 |
2.7 |
-4.712 |
-1.192 |
1.076 |
— |
— |
— |
| 4 |
3.5 |
-5.904 |
-0.116 |
— |
— |
— |
— |
| 5 |
4.3 |
-6.02 |
— |
— |
— |
— |
— |
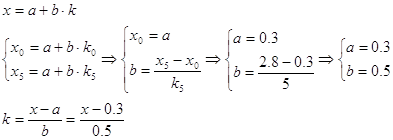
Найдем формулу перехода от x
к k:
Выполним проверку, вычислив
аналитически конечную разность
Δng(x)= ΔnG(k) для n = 5:
Конечные разности,
вычисленные аналитически и таблично Δng(x) = ΔnG(k) для n = 5 совпали,
следовательно, таблица повторных разностей составлена верно.
Задача 3
Таблично заданную функцию G(k)
с целочисленным аргументом представить в виде разложения по факториальным
многочленам (z(n) = z · (z-1) · (z-2) · … · (z - n + 1)) и преобразовать его в степенные
многочлены G(z) и G(x).
Решение
Представим
функцию G(k) в виде разложения по факториальным многочленам:
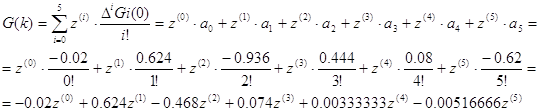
Преобразуем функцию G(k) в степенной многочлен G(z):
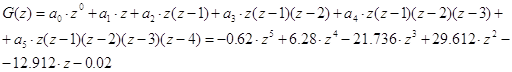
Выполним проверку при k = 1:
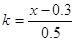
0.604=0.604
Так как результаты
совпали, значит степенной многочлен G(z) представлен правильно.
Преобразуем функцию G(k) в степенной многочлен G(x). Зная, что получим:
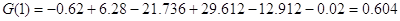
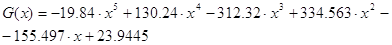
Проверим вычисления при x = 0.8:
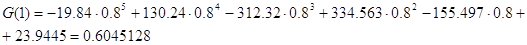
0.6045128 ≈ 0.604
Так как результаты
совпали, то вычисления сделаны верно.
Задача 4
Вывести аналитическое
выражение суммы для функции целочисленного аргумента G(z). Проверить правильность вычисления полученного
выражения прямым суммированием табличных значений G(k), k = 0,
1, 2, 3, 4, 5 (m = 5).
Решение.
Для вычисления значения
суммы используем функцию G(z) в виде разложения по факториальным многочленам,
полученным в задаче 3:
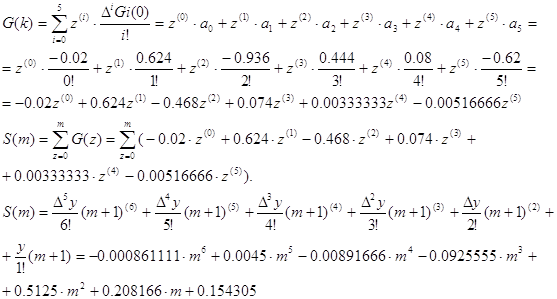
где
Для проверки, просуммируем значения G(k) из таблицы:
-0.02 + 0.604 + 0.292 -
0.512 - 1.284 - 2.04 = - 2.96
- 2.96 = - 2.96
Так как результаты
вычисления аналитического выражения и суммы табличных значений G(k) совпали, значит аналитическое выражение для суммы
выведено правильно.
Задача 5
Составить таблицу упорядоченных
разделенных разностей для g(x). Проверить правильность таблицы для разделенной
разности [x0; x1; x2; x3] по
формуле ее аналитического представления.
Решение
Составим таблицу
упорядоченных разделенных разностей для g(x):
|
xi
|
g(xi)
|
[xi; xi+1]
|
[xi; xi+1; xi+2]
|
[xi; xi+1; xi+2; xi+3]
|
[xi; xi+1; xi+2; xi+3; xi+4]
|
[xi; xi+1; xi+2; xi+3; xi+4;xi+5]
|
| 0.3 |
-0.02 |
1.248 |
-1.872 |
0.592 |
0.0533333 |
-0.1567999 |
| 0.8 |
0.604 |
-0.624 |
-0.984 |
0.6986666 |
-0.3386666 |
— |
| 1.3 |
0.292 |
-1.608 |
0.064 |
-0.0213333 |
— |
— |
| 1.8 |
-0.512 |
-1.544 |
0.032 |
— |
— |
— |
| 2.3 |
-1.284 |
-1.512 |
— |
— |
— |
— |
| 2.8 |
-2.04 |
— |
— |
— |
— |
— |
Для проверки правильности заполнения
таблицы разделенных разностей, вычислим разделенную разность пятого порядка по
формуле ее аналитического представления:
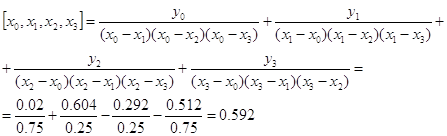
Так как результаты
вычислений совпали, значит, таблица разделенных разностей составлена правильно.
Задача 6
Получить интерполяционные
многочлены Лагранжа и Ньютона, проходящие через первые четыре точки таблично
заданной функции G(x), и сравнить их степенные
представления.
Решение
Для нахождения
интерполяционного многочлена Лагранжа используем формулу
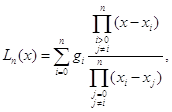 где n = 3.
где n = 3.
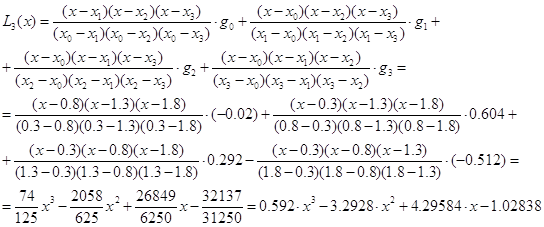
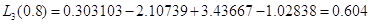
Проведем проверку вычислений,
подставив x=0.8 в интерполяционный многочлен
Лагранжа, получим y1=0.604
Интерполяционный многочлен Ньютона
находится по формуле:
ln(x)
= g0 + (x-x0)[x0;x1] + (x-x0)(x-x1)[x0;x1;x2]
+ … +
+(x-x0)(x-x1)∙
…∙(x-xn-1)[x0;x1;x2;…;xn]
Подставив в формулу gi и xi получим:
Интерполяционные
многочлены Ньютона и Лагранжа совпадают.
Проведем проверку вычислений,
подставив x=0.8 в интерполяционный многочлен
Ньютона, получим y1=0.604
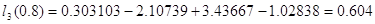
Задача 7.
Вывести выражения для вычисления
второй производной в точке x=x3 в виде функций:
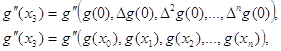
где ∆ng(0)
и g(xn) для n = 0,1,…,5 соответственно значения
разностей в точке x = x0 и ординаты g(xn) = gn
из задачи N2. Значения производной вычисленные по выведенным формулам, сравнить
с вычисленным значением производной, найденной путем дифференцирования
интерполяционного многочлена G(x):
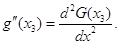
Решение
Для вычисления производной
воспользуемся оператором
дифференцирования:
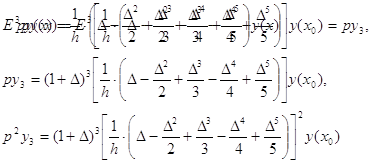
Выражение для вычисления производной в
точке x0 имеет вид:
Для того, чтобы преобразовать его к
выражению для вычисления производной в точке x3, применим оператор
сдвига:
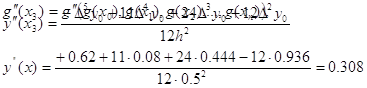
Для того, чтобы перейти от функции к
функции воспользуемся формулой:
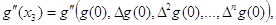
Получим выражения для ∆2y0:
∆5y0
= -y0 + 5y1 – 10y2 + 10y3 –
5y4 + y5
∆4y0
= y0 - 4y1 + 6y2 - 4y3 + y4
∆3y0
= -y0 + 3y1 – 3y2 + y3
∆2y0
= y0 - 2y1 + y2
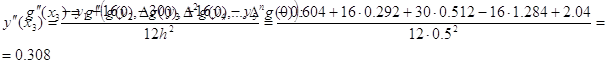
Подставим эти значения в
функцию:
Сравним это значение с вычисленным
значением производной путем дифференцирования интерполяционного многочлена G(x):
при x3 = 1.8
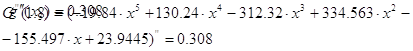
Значения производной равны,
следовательно, вычисления сделаны верно.
Задача 8
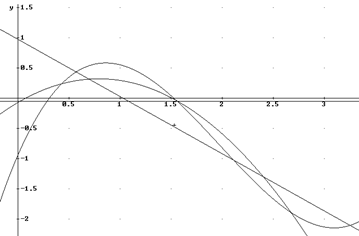
Методом наименьших
квадратов для таблично заданной g(x) получить
аппроксимирующие степенные полиномы нулевой, первой, второй и третьей степеней (Pi(x), i = 0, 1, 2, 3) и изобразить их на одном графике.
Решение.
Составим таблицу степеней
x и xy
| i |
x |
y |
x2
|
x3
|
x4
|
x5
|
x6
|
xy |
x2y
|
x3y
|
| 1 |
0.3 |
-0.02 |
0.09 |
0.027 |
0.0081 |
0.00243 |
0.000728999 |
-0.006 |
-0.0018 |
-0.00054 |
| 1 |
0.8 |
0.604 |
0.64 |
0.512 |
0.4096 |
0.32768 |
0.262144 |
0.4832 |
0.38656 |
0.309247 |
| 1 |
1.3 |
0.292 |
1.69 |
2.197 |
2.8561 |
3.71293 |
4.8268 |
0.3796 |
0.493479 |
0.641523 |
| 1 |
1.8 |
-0.512 |
3.24 |
5.832 |
10.4976 |
18.8956 |
34.0122 |
-0.9216 |
-1.65888 |
-2.98598 |
| 1 |
2.3 |
-1.284 |
5.29 |
12.167 |
27.9840 |
64.3634 |
148.035 |
-2.9532 |
-6.79236 |
-15.6224 |
| 1 |
2.8 |
-2.04 |
7.84 |
21.952 |
61.4656 |
172.103 |
481.89 |
-5.712 |
-15.9936 |
-44.782 |
| 6 |
9.3 |
-2.96 |
18.79 |
42.687 |
103.22 |
259.405 |
669.026 |
-8.73 |
-23.5666 |
-62.4401 |
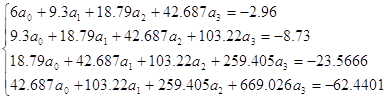
Составим системы уравнений:
Откуда a0 = -0.93621; a1
= 3.89576; a2 = -2.8954; a3 = 0.488001
Аппроксимирующий степенной полином 3-й
степени имеет вид:
P3(x)
= -0.93621 + 3.89576x – 2.8954x2 + 0.488001x3
Откуда a0 = -0.0710314; a1
= 0.989486; a2 = -0.624589;
Аппроксимирующий степенной полином 2-й
степени имеет вид:
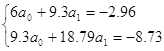
P2(x)
= -0.0710314 + 0.989486x – 0.624589x2
Откуда a0 = 0.974118; a1
= -0.946742;
Аппроксимирующий степенной полином 1-й
степени имеет вид:
P1(x)
= 0.974118 – 0.946742x
6a0
= -2.96
Откуда a0 = -0.493333;
Аппроксимирующий степенной полином 0-й
степени имеет вид:
P0(x) =
-0.0493333
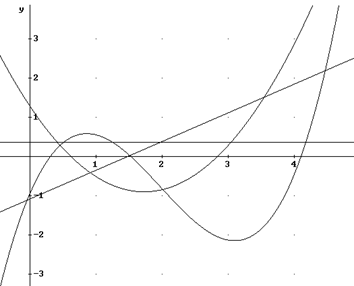
Изобразим полученные полиномы на
графике:
Задача 9
Для аппроксимирующего
полинома третьей степени P3(x) получить аналитические выражения ΔnP3(x), n = 0, 1, 2, 3, 4 и все конечно-разностные разностные
кривые изобразить на одном графике.
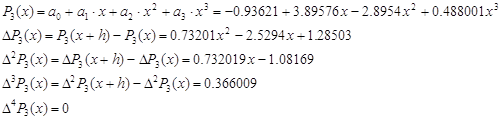
Решение
Обозначим на графике все
конечно-разностные кривые:
Задача 10
Вывести квадратурные
формулы для вычисления определенных интегралов с пределами [0, 1] и [-1, 1] от
подынтегральных функций f(t), принадлежащих классу степенных
многочленов степеней 0, 1, 2, 3. Вывод проделать для трех случаев использование
в квадратурных формулах численных значений подынтегральных функций:

в) заданы значения функции в
точках, обеспечивающих получение формул наивысшей алгебраической степени точности.
Решение
Значение определенного
интеграла найдем, исходя из формулы:
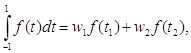
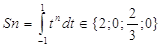
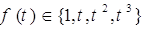
где w1, w2
— некоторые коэффициенты
t1, t2 —
точки, плавающие внутри интервала интегрирования.
Составим систему уравнений
w(t) = (t-t1)(t-t2)
= C0 + C1t + C2t2 = 0
C2 = 1
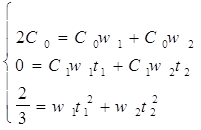
Домножив уравнения на
соответствующие коэффициенты получим:
2C0
+ 2/3 = w1 (C0 + C1t1 + t12)
+ w2 (C0 + C1t1 + t22)
2C0+ 2/3 = 0
C0 = -1/3

Подставляя полученные значения
в первую систему, получим:
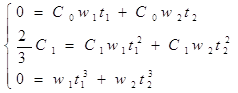
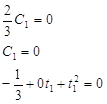
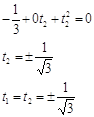
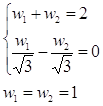
Квадратурная формула: 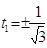
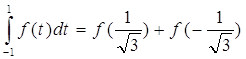
Задача 11
С помощью квадратурных
формул, полученных в задаче 10, вычислить определенный интеграл от степенного
представления интерполяционного многочлена Лагранжа (Ньютона), полученного в
задаче № 6 в пределах от x0 до x0 +3h, и
сравнить его с аналитически вычисленным значением определенного интеграла по
первообразным многочлена.
Решение
Используем степенное
представление интерполяционного многочлена Лагранжа из задачи 6
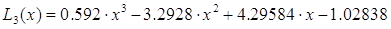
Для перехода к интегралу
с канонической формой используем линейное преобразование: x = α + βt.
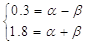
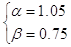
Составим систему
уравнений:
Подставив x = 1.05 + 0.75t, получим многочлен Лагранжа от
переменной t:
L (t) = 0.24975t3
- 0.80325t2 - 0.49575t + 0.537253
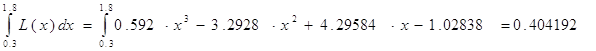
Учитывая, что dx = βdt, получим:
Применим квадратурную
формулу, полученную в задаче №10
Для сравнения вычислим
аналитически значение интеграла:
Так как результаты
совпали, значит, вычисления произведены верно.
Задача 12
Оценить погрешность
определенного интеграла от функции sin(x) в пределах [0,2/3π] по
квадратурной формуле наивысшей алгебраической степени точности, полученной в
задаче № 10в, по сравнению с аналитически точным. Проделать то же самое над
усеченным степенным рядом, представляющим sin(x), в
который x входит со степенью не выше третьей.
Решение
Перейдем от пределов [0,2/3 π] к пределу [-1,1]: для этого
воспользуемся линейным преобразованием x= α + βt . Составить систему
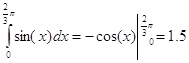
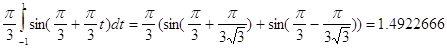
Учитывая, что dx = βdt, получим:
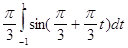
Применим квадратурную
формулу:
Вычислим аналитически:
Найдем погрешность
вычисления:
Проделаем те же операции
над усеченным степенным рядом, представляющем sin(x):
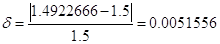
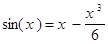
Перейдем от пределов [0;
2π/3] к пределам [-1; 1], для этого
используем линейное преобразование x = α +βt. Составим систему уравнений:
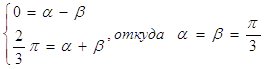
Учитывая, что dx = βdt,
получим

Применим квадратурную формулу,
получим
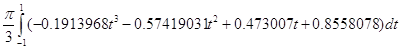
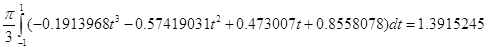
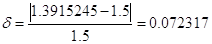

Найдем погрешность вычисления
Задача 14
Степенными полиномами
Чебышева Ti относительно переменной x (|x| < 1) являются решениями линейного разностного уравнения
второго порядка:
Ti+2
- 2x Ti+1 + Ti = 0,
с начальными условиями T0 = 1 и T1 = x.
Найти аналитическое
выражение и вычислить значения полинома Чебышева i-й степени, если 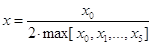 и i = 4. Проверить вычисления непосредственно по
заданной рекуррентной формуле. Найти положение нулей и экстремумов у
многочленов Чебышева в общем виде и для заданных выше x и i. Оценить модуль
максимально возможного значения полинома в точках экстремумов.
и i = 4. Проверить вычисления непосредственно по
заданной рекуррентной формуле. Найти положение нулей и экстремумов у
многочленов Чебышева в общем виде и для заданных выше x и i. Оценить модуль
максимально возможного значения полинома в точках экстремумов.

Решение.
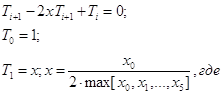
Исходя из того, что
xi = |yi| надо найти T4 т.е. для i = 4
Из Ti+2 - 2xTi+1 + Ti = 0 следует, что
T2
= 2xT1 - T0
T3
= 2xT2 - T1 = 2x(2xT1 - T0) - T1
T4
= 2xT3 - T2 = 2x(2x(2xT1 - T0) - T1)
- 2xT1 + T0 = 8x3T1 - 4x2T0
- 4xT1 + T0
Подставим значение T0 = 1 и T1 = x
T4
= 8x4 - 4x2 - 4x2 + 1 = 8x4 - 8x2
+ 1
Найдем значения x:
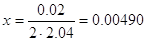
T4 = 0.99980
Проверим по заданной
рекуррентной формуле:
T2
= 2·0.00490·0.00490 - 1 = -0.9999
T3
= 2·0.00490·(-0.9999) - 0.00490 = -0.01469
T4
= 2·0.00490·(-0.01469) + 0.9999 = 0.99980
Нули функции находятся,
как решения биквадратного уравнения:
8x4 - 8x2 + 1 = 0, где
x1 = 0.9238795
x2 = -0.9238795
x3 = 0.3826834
x4 = -0.3826834
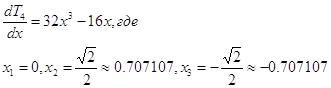
Чтобы найти экстремумы
найдем
Задача 16
Выравнивание по всей
длине с течением времени температуры T(x, t) на тонком однородном хорошо теплоизолированном стержне описывается
дифференциальным уравнением в частных производных с начальным распределением
температуры (в градусах Цельсия) по длине стержня в 6 равномерно расположенных
с шагом h точках.
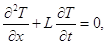
T(x0,
0) = T0, T(x1, 0) = T1, …, T(x5,
0) = T5; (Ti = 100·yi ˚C).
На концах стержня в
точках x-1 и x6 удерживается нулевая температура.
Применяя
конечно-разностное представление производных по пространственной переменной x, свести уравнение в частных
производных к системе дифференциальных уравнений в обыкновенных производных
относительно температуры T.
Решение.

Получаем систему диф.
уравнений:
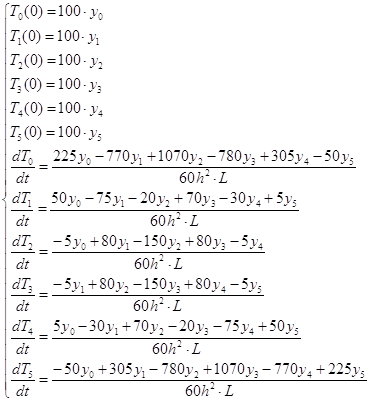
Учитывая начальные
условия, получим систему уравнений:
Задача 17.
Используя метод
Ньютона-Рафсона, найти с относительной погрешностью в одну миллионную нуль
многочлена Чебышева Ti(x), полученного в задаче 14. В качестве
начального приближения к корню взять
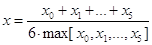
В качестве xi
берутся |yi| из таблицы исходных данных.
Решение.
Из задачи 14 возьмем
полином Чебышева T4 = 8x4 - 8x2 + 1. В
качестве начального приближения к корню возьмем xнач, вычисленное по
формуле
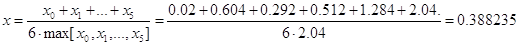
Т.к. 8x4 - 8x2
+ 1 = 0, то можем сказать, что f(xнач + α) = 0
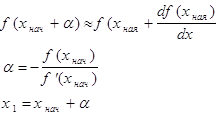
Воспользуемся DERIVE для
нахождения корня с необходимой точностью:
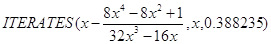
получим такие значения:
0.38234, 0.382689, 0.382683, 0.382683, 0.382683.
На третьей итерации
получаются значения корня с нужной точностью.
Задача 19
Скорость изменения
переменной x(t) во времени равна функции от этой переменной f(x). Найти
аналитическое выражение последней от времени, начиная с t = 0, если в начальный
момент x(0) = 0. В качестве f(x) взять степенной многочлен P2(x),
полученный в задаче 8. Протабулировать полученное решение с шагом h = 0.1 в
интервале [0, 0.5].
Решение
P2(x) =
-0.0710314 + 0.989486x – 0.624589x2
= f(x)
Исходя из начальных
условий, т.к. dx/dt = f(x), имеем
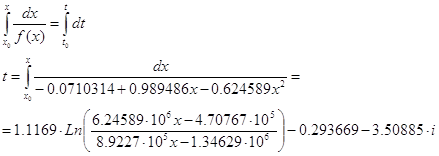
Т.к. x = F(t), то:
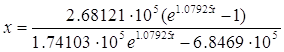
Протабулируем x(t) на
интервале [0; 0.5] c шагом h = 0.1:
t = 0 x
= 0
t = 0.1 x =
-0.0622648
t = 0.2 x =
-0.137833
t = 0.3 x =
-0.230872
t = 0.4 x =
-0.347464
t = 0.5 x =
-0.496850
Задача 20
Методом Эйлера в
интервале [0, 0.5] с шагом h = 0.1 получить решение нелинейного
дифференциального уравнения:
dx/dt = a + bx
+ cx2,
x(0) = 0
Коэффициенты a, b, c
взять из P2(x), полученного в задаче 8.
Решение
y = P2(x)
P2(x)
= -0.0710314 + 0.989486x – 0.624589x2
Общая формула для решения
x = x0 +
h·P2(x0, t0)
x1
= 0 + 0.5· (-0.0710314) = -0.0355156
x2
= -0.0355156 + 0.5·(-0.0710314 + 0.989486 (-0.0355156)1 –
-0.624589·
(-0.03551562) = -0.053854
x3
= -0.053854 + 0.5· (-0.0710314 + 0.989486 (-0.053854)1 –
- 0.624589 (-0.053854)2)
= -0.0636315
x4 =
-0.0636315 + 0.5· (-0.0710314 + 0.989486 (-0.0636315)1 –
-0.624589 (-0.0636315)2)
= -0.0689304
x5 =
-0.0689304 + 0.5 (-0.0710314 + 0.989486 (-0.0689304)1 –
-0. 0.624589 (-0.0689304)2)
=--0.071827
Задача 23
Проверить заданную
систему из трех векторов на линейную зависимость. При обнаружении линейной
зависимости поменять местами первые компоненты векторов x1,x2 и выполнить
повторную проверку. Из исходных данных векторы формируются так:
x1 =
(y0,y1,y2); x2=(y3,y4,y5);
x3=(h,x0,0).
На базе линейно
независимой системы векторов x1, x2, x3 методом
Грама-Шмидта построить ортонормированную систему трех векторов:
y1 =
(y11,y21,y31); y2=(y12,y22,y32);
y3=(y13,y23,y33).
На основе полученной
системы векторов сформировать квадратную матрицу T = (y1,y2,
y3). Вычислить det(T) и получить матрицы — обратную T-1 и
транспонированную T’. Найти произведение T-1 · T, T · T’. Сделать
выводы о свойствах матрицы T.
Решение
Исходные векторы x1 =
(-0.02,0.604,0.292); x2=(-0.512,-1.284,-2.04);
x3=(0.5,0.3,0).
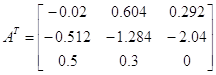
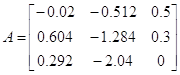
Составим матрицу и
проверим ее на линейную зависимость:
det (A·AT) =
0.23591 > 0, значит система линейно независима.
Найдем векторы v1,
v2, v3
 v1 = x1
v1 = x1
v2
= x2 + a21·v1
v3
= x3 + a32·v2 + a31·v1
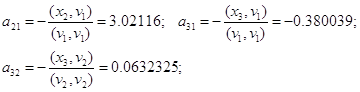
v1
= (-0.02, 0.604, 0.292);
v2
= (-0.572423, 0.54078, -1.15782);
v3 =
(0.471405, 0.104651, -0.184183).
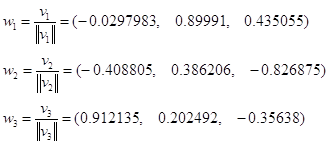
Матрица T:
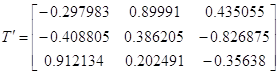
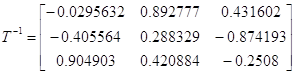
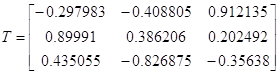
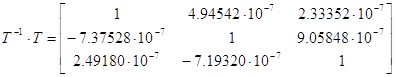
det(T) = -1
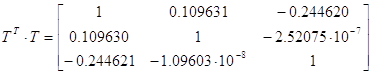
Ортонормированная матрица
T состоит из собственных векторов. Определитель матрицы T равен 1. Если
транспонировать ортогональную матрицу то она будет равна обратной. T’ = T-1.
Это значит, что если умножить T·T’ = E — получим единичную матрицу.
Задача 24
Считая числа –1, -2, -3
собственными значениями, а векторы у1, у2, у3
из задачи 23 – собственными векторами некоторой матрицы А, найдите проекторы
этой матрицы ( Р1, Р2, Р3), саму матрицу А и
ей обратную А-1. Получить характеристическое уравнение матрицы А и
подтвердить правильность всех промежуточных вычислений.
Решение
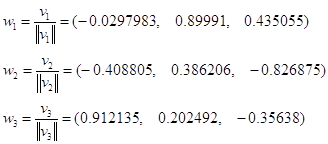
Найдем проекторы матрицы
А:
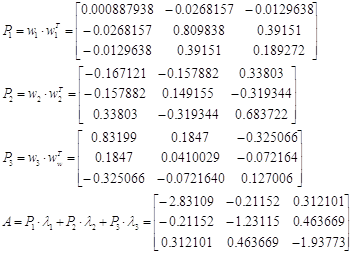
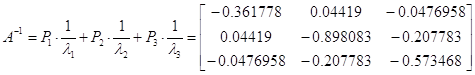
Найдем обратную матрицу А-1:
Характеристическое
уравнение матрицы А имеет вид:
-x3-6x2-11x-6=0;
Корни характеристического
уравнения – собственные значения матрицы
x1= -1; x2=
-2; x3= -3
Задача 25
Решить систему
алгебраических уравнений А·x = b, где А- матрица коэффициентов из задачи 24, x
= (x1, x2, x3) – векторы решения, b = (3, 2, 1) – вектор правых частей. Решение
получить, используя обратную матрицу, полученную из задачи 24.
Решение

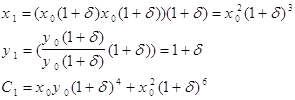
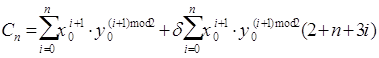
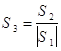
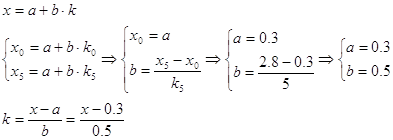
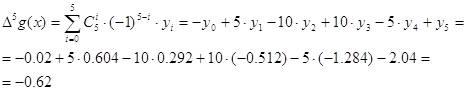
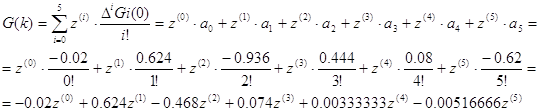
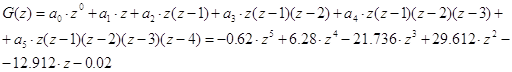
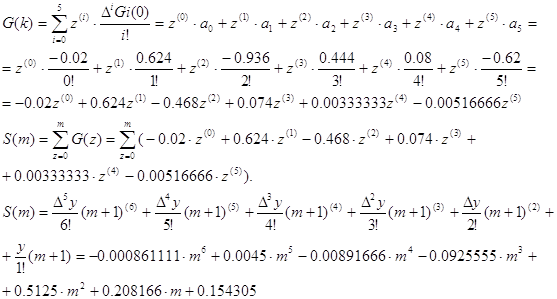
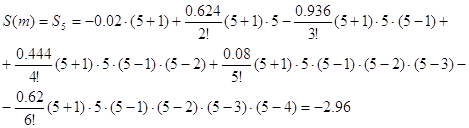
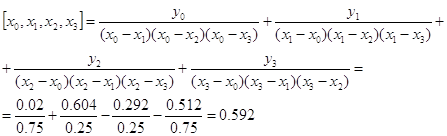
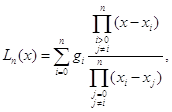 где n = 3.
где n = 3.