Контрольная работа: Моделювання економічних та виробничих процесів

МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

Бердичівський політехнічний коледж

Контрольна робота

з дисципліни

“Моделювання економічних та виробничих процесів”

(варіант №12)

Виконала:

студентка групи Пзс-604

Побережний Дмитро Валерійович

Перевірив:

викладач

Тростянський Борис Геннадійович

м. Бердичів

2007 р.

Завдання 1

Процес виготовлення двох видів промислових виробів складається в послідовній обробці кожного виробу на трьох верстатах. Час використання цих верстатів для виробництва цих виробів обмежений 10 – ю годинами на добу. Час обробки та прибуток від продажу одного виробу наведені у таблиці:

Виріб	Час одного виробу, хвил.			Прибуток, гош.од.
Виріб	Верстат 1	Верстат 2	Верстат 3	Прибуток, гош.од.
1	10	6	8	2
2	5	20	15	3

Найти оптимальний обсяг виробництва виробу кожного типу.

Розв'язок:

Записуємо математичну модель задачі.

Позначимо відповідно х1, х2 кількість виробів кожного виду.

Система обмежувальних умов має наступний вигляд:

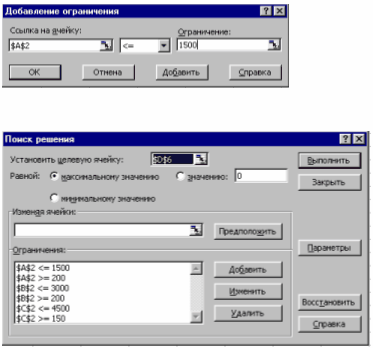
2*х1+3*х2+5*х3<=4000

4*х1+2*х2+7*х3<=6000

х1<=1500

x2<=3000

x3<=4500

x1>=200

x2>=200

x3>=150

Цільова функція має вигляд F=30*х1+20*х2+50*х3 → max

Модель даних у MS Exel має вигляд:

Викликаємо “Поиск решений” та заносимо усі обмеження:

Після чого знаходимо рішення:

Відповідь: максимальний прибуток (330000 гр. од.) буде досягнуто при випуску виробів трьох моделей у кількості 1500, 3000, 4500 відповідно.

Завдання 2

Є n робітників та m видів робіт. Вартості Ci,j виконання i – тим робітником j – тої роботи наведені в таблиці, де робітнику відповідає рядок, а роботі стовпчик. Потрібно скласти план робіт так, що б всі роботи були виконані, кожний робітник був зайнятий тільки на одній роботі, а вартість виконання всіх робіт була мінімальною.

№ робітника	Вартість виконання кожної роботи
№ робітника	1	2	3	4
1	1	3	6	5
2	5	2	7	8
3	3	5	1	9
4	6	4	2	10

Розв'язок:

Для складання плану робіт у MS Exel визначимо область даних того ж розміру що й таблиця вартості робіт кожним робітником:

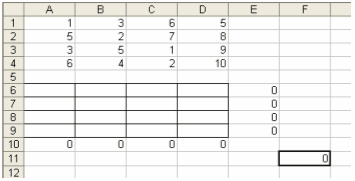
В цій області відображатиметься яку роботу буде виконувати кожний працівник. «Одиниця» робота виконується, а «нуль» - ні.

Так як необхідно щоб всі роботи були виконанні та кожен робітник був зайнятий тільки на одній роботи, то суми у кожному стовпчику і рядку мають дорівнювати 1:

$A$10 : $D$10 = 1;

$E$6 : $E$9 = 1.

Це буде першим обмеженням.

Друге обмеження полягає в тому, що значення середині області можуть бути 1 або 0, отже:

$A$6 : $D$9 = 0;

$A$6 : $D$9 = 1;

$A$6 : $D$9 = целое.

Цільова функція у MS Exel матиме вигляд:

F11 = СУММПРОИЗВ(A1:D4;A6:D9) → min.

Викликаємо “Поиск решений”, вказуємо цільову комірку та заносимо усі обмеження:

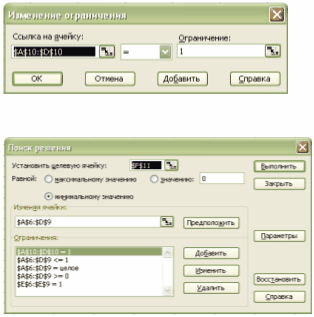
Після чого знаходимо рішення:

Відповідь: 1 робітник робить 4 роботу;

2 робітник робить 2 роботу;

3 робітник робить 1 роботу;

4 робітник робить 3 роботу.

При цьому витрати на виконання всіх робіт будуть мінімальними. Вони становитимуть 12 грошових одиниць.

Завдання 3

Є n пунктів виробництва та m пунктів розподілу продукції. Вартість перевезення одиниці продукції з і-го пункту виробництва і j-й центр розподілу сіj приведена в таблиці, де під рядком розуміється пункт виробництва, а під стовпчиком – пункт розподілу. Крім того, в цій таблиці в і-му рядку вказано об’єм виробництва в і-му пункті виробництва, а в j-му стовпчику вказано попит в j-му центрі розподілу.

Необхідно розробити математичну модель та план перевезень по доставках необхідної продукції в пункти розподілу, який мінімізує сумарні транспортні витрати.

Варіант 2	Вартість перевезення одиниці продукції				Об’єми виробництва
	2	7	7	6	20
	1	1	1	2	50
	5	5	3	1	10
	2	8	1	4	20
Об’єми використання	3	2	1	5	10

Розв'язок:

Переносимо данні вартості перевезень одиниці продукції з умови у MS Exel. Виділяємо область даних для знаходження плану перевезень:

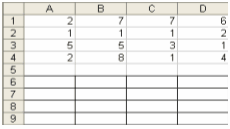
Напроти кожного рядка та стовпчика виділяємо по комірці, у яких відображатиметься сумарна кількість продукції по пунктам виробництва та обсягам виробництва для подальшої перевірки можливості розподілу.

Використовуємо функцію СУММ із завданням діапазону комірок відповідного рядка та стовпчика - =СУММ(A6:D6):

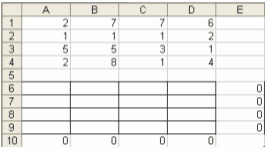
У наступних, за цими, комірками вносимо значення об’ємів виробництва та використання:

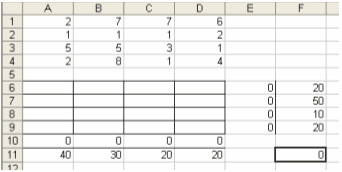
Комірку F11 виділяємо для цільової функції, у яку записуємо формулу: =СУММПРОИЗВ(A1:D4;A6:D9):

Обмеженням для вирішення цієї задачі буде те, що значення комірок у яких підраховується сума по рядкам і стовпчикам має дорівнювати значенням занесеними з умови задачі.

Крім цього, звісно, область виділена для плану перевезень має бути більшою нуля.

Викликаємо “Поиск решений”, вказуємо цільову комірку та заносимо усі обмеження:

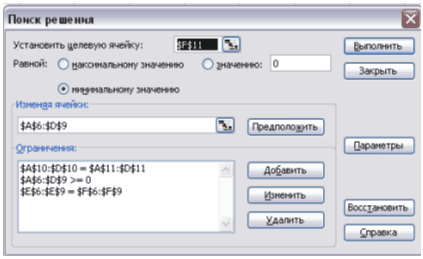
Натискаємо кнопку «Выполнить» та отримуємо рішення нашої транспортної задачі:

Відповідь: розроблений план перевезень дає можливість отримати мінімальні витрати у розмірі 237,5 грошових одиниць

Завдання 4

Побудувати лінійну модель регресивного аналізу для економічного показника, зміни якого спостерігалися в певному інтервалі часу.

Контрольний термін	1	2	3	4	5	6	7	8	9	10
Значення показника	9	16	20	27	34	39	44	52	58	64

Розв'язок:

Заносимо Контрольний термін і Значення показника у комірки MS Exel

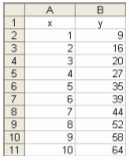
На основі даних умови будуємо графік:

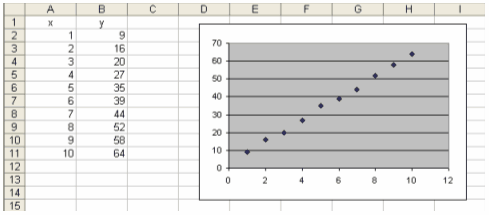
Додаємо до графіка лінію тренда різних типів та записуємо величину достовірності:

Лінійна лінія тренду:

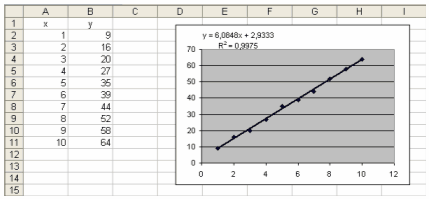
R2 = 0,9975;

Логарифмічна:

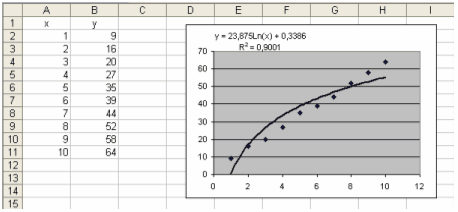
R2 =0,9001;

Поліноміальна:

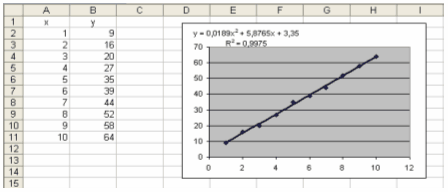
R2 =0,9975;

Степенева:

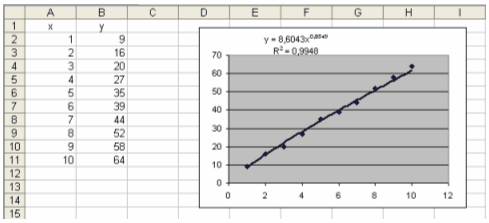
R2 =0,9948;

Експоненціальна:

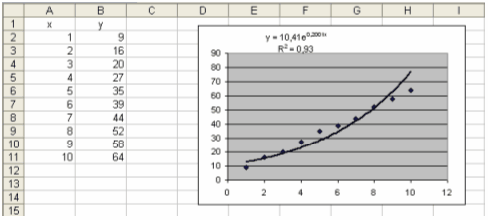
R2 =0,93.

Проаналізувавши величини достовірності, визначаємо що найбільша точність при лінійній та поліноміальній лінії тренда (R2 =0,9975). Так як функція при лінійній лінії тренду легша для сприймання та підрахунку ніж при поліноміальній, то використовувати будемо саме її:

y = 6,0848х+2,9333.

Це і є лінійна модель регресивного аналізу для економічного показника, зміни якого спостерігалися в певному інтервалі часу.

За «х» приймаємо Контрольний термін. Записуємо функцію комірки MS Exel з посиланням на Контрольний термін замість «х».

Продовжуючи зростання значення Контрольного терміну і використовуючи цю функцію отримуємо наступні значення показника:

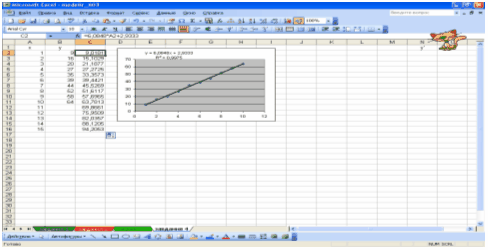
Відповідь: лінійна модель регресивного аналізу: y = 6,0848х+2,9333.

Список використаної літератури

1. Гарнаев А., «Использование MS Excel и VBA в экономике и финансах».

2. А.И. Ларионов, «Экономико-математические методы в планировании».

3. Конспект лекцій.