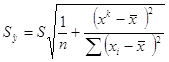- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Контрольная работа: Парная регрессияКонтрольная работа: Парная регрессияКонтрольная работа по теме: "Парная линейная регрессия" Данные, характеризующие прибыль торговой компании "Все для себя" за первые 10 месяцев 2004 года (в тыс. руб.), даны в следующей таблице:
В контрольной работе с использованием табличного процессора Ехсеl необходимо выполнить следующие вычисления и построения: 1. Построить диаграмму рассеяния. 2. Убедится в наличии тенденции (тренда) в заданных значениях прибыли фирмы и возможности принятия гипотезы о линейном тренде. 3.
Построить линейную парную регрессию (регрессию вида 4. Нанести график регрессии на диаграмму рассеяния. 5. Вычислить значения статистики F и коэффициента детерминации R2. Проверить гипотезу о значимости построенного уравнения регрессии. 6. Вычислить выборочный коэффициент корреляции и проверить гипотезу о ненулевом его значении. 7. Вычислить оценку дисперсии случайной составляющей эконометрической модели. 8. Проверить гипотезы о значимости вычисленных коэффициентов b0, b1 . 9. Построить доверительные интервалы для коэффициентов b0, b1. 10. Построить доверительные интервалы для дисперсии случайной составляющей эконометрической модели. 11.
Построить доверительную область для условного математического ожидания М( 12. С
помощью линейной парной регрессии сделать прогноз величины прибыли на ноябрь и
декабрь месяц и нанести эти значения на диаграмму рассеяния. Сопоставить эти
значения с границами доверительной области для условного математического
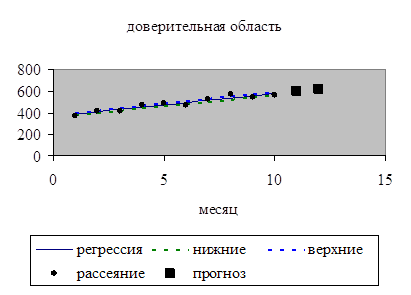
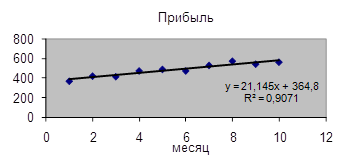
ожидания М( Решение. Используя исходные данные, строим диаграмму рассеяния:
На основе анализа диаграммы рассеяния убеждаемся в наличии тенденции увеличения прибыли фирмы и выдвигаем гипотезу о линейном тренде. Полагаем, что связь между факторами Х и У может быть
описана линейной функцией
b0 n + b1 Уxi = Уyi, b0 Уxi + b1 Уxi2 = Уxiyi. Составляем вспомогательную таблицу:
Для нашей задачи система имеет вид:
Решение этой системы можно получить по правилу Крамера:
Получаем:
Таким образом, искомое уравнение регрессии имеет вид: y =364,8 + 21,145x. 4. Нанесем график регрессии на диаграмму рассеяния.
5. Вычислим значения статистики F и коэффициента детерминации R2. Коэффициент детерминации рассчитаем по формуле R2 = rxy2 = 0,9522 = 0,907. Проверим адекватность модели (уравнения регрессии) в целом с помощью F-критерия. Рассчитаем значение статистики F через коэффициент детерминации R2 по формуле:
Получаем: Fфакт. > F0,01;1;8, т.к. 78,098 > 11,26. Следовательно, делаем вывод о значимости уравнения регрессии при 99% - м уровне значимости. 6. Вычислим выборочный коэффициент корреляции и проверим гипотезу о ненулевом его значении. Рассчитаем выборочный коэффициент корреляции по формуле:
Получаем:
Проверка существенности
отличия коэффициента корреляции от нуля проводится по схеме: если Здесь t1-б/2,n-2 – квантиль распределения Стьюдента, б - уровень значимости или уровень доверия, n – число наблюдений, (n-2) – число степеней свободы. Значение б задается. Примем б = 0,05, тогда t1-б/2,n-2 = t0,975,8 = 2,37. Получаем:
Следовательно, коэффициент корреляции существенно отличается от нуля и существует сильная линейная связь между х и у. С использованием табличного процессора Ехсеl проведем регрессионную статистику: Вывод итогов:
Вычисленные значения коэффициентов b0, b1, значения статистики F, коэффициента детерминации R2 выборочного коэффициента корреляции rxy совпадают с выделенными в таблице. 7.
Оценка дисперсии случайной составляющей эконометрической модели вычисляется по
формуле Используя результаты регрессионной статистики, получаем:
8. Проверим значимость вычисленных коэффициентов b0, b1 по t-критерию Стьюдента. Для этого проверяем выполнение неравенств:
где
Используем результаты регрессионной статистики:
Получаем: Так как 9. Доверительные интервалы для коэффициентов b0, b1 получаем с помощью результатов регрессионной статистики. Доверительный интервал для коэффициента b0 уравнения регрессии:
Доверительный интервал для коэффициента b1 уравнения регрессии:
10. Построим доверительный интервал для дисперсии случайной составляющей эконометрической модели по формуле:
Примем б = 0,05, тогда по таблице для 10-элементной выборки q = 0,65. Получаем:
11.
Построим доверительную область для условного математического ожидания М( Доверительные интервалы для
уравнения линейной регрессии:
где
Рассмотрим уравнение: y
=364,8 + 21,145x. Пусть
График уравнения регрессии, доверительная полоса, диаграмма рассеяния:
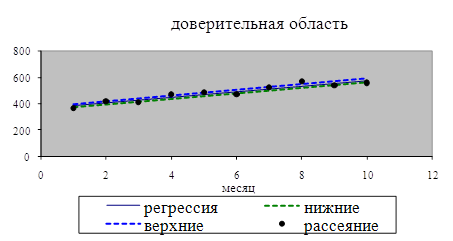
12. С помощью линейной парной регрессии сделаем прогноз величины прибыли на ноябрь и декабрь месяц:
Нанесем эти значения на диаграмму рассеяния.
Эти
значения сопоставимы с границами доверительной области для условного
математического ожидания М( Точность прогнозирования: с вероятностью 0,95 прибыль в ноябре находится в интервале (487,292; 515,508); прибыль в декабре находится в интервале (497,152; 526,376). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
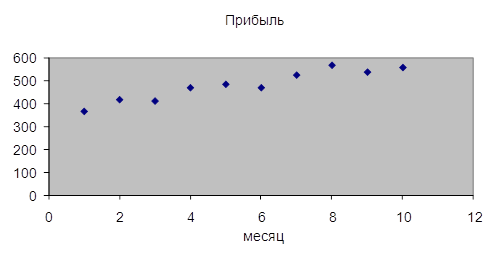
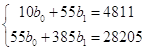
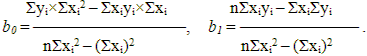
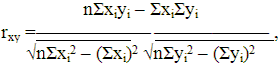
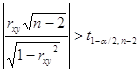 , то гипотеза о
существенном отличии коэффициента корреляции от нуля принимается, в противном
случае отвергается.
, то гипотеза о
существенном отличии коэффициента корреляции от нуля принимается, в противном
случае отвергается.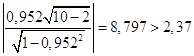 .
.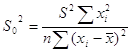 ,
, 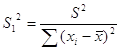 .
.