Контрольная работа: Применение методов линейного программирования для оптимизации стоимости перевозок

Контрольная работа: Применение методов линейного программирования для оптимизации стоимости перевозок

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Реферат

по дисциплине: Методы и модели в экономике и менеджменте.

на тему: «Применение методов линейного программирования для оптимизации стоимости перевозок»

Воронеж 2010

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

В общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с  баз   потребителям .

Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).

(3. )

Обозначим количество груза, имеющегося на каждой из  баз (запасы), соответственно ,а общее количество имеющегося в наличии груза–:

;

(3. )

заказы каждого из потребителей (потребности) обозначим соответственно, а общее количество потребностей – :

,

(3. )

Тогда при условии

(3. )

мы имеем закрытую модель, а при условии

– открытую модель транспортной задачи.

Очевидно, в случае закрытой модели весь имеющийся в наличии груз развозится полностью, и все потребности заказчиков полностью удовлетворены; в случае же открытой модели либо все заказчики удовлетворены и при этом на некоторых базах остаются излишки груза , либо весь груз оказывается израсходованным, хотя потребности полностью не удовлетворены .

Так же существуют одноэтапные модели задач, где перевозка осуществляется напрямую от, например, базы или завода изготовителя к потребителю, и двухэтапные, где между ними имеется “перевалочный пункт”, например – склад.

План перевозок с указанием запасов и потребностей удобно записывать в виде следующей таблицы, называемой таблицей перевозок (Таблица 3. ):

Таблица 3. - План перевозок с указанием запасов и потребностей

Пункты Отправления	Пункты назначения				Запасы
			…
			…
			…
…	…	…	…	…	…
			…
Потребности			…		или

Условие  или  означает, с какой задачей мы имеем дело, с закрытой моделью или открытой моделью транспортной задачи. Переменное  означает количество груза, перевозимого с базы  потребителю : совокупность этих величин образует матрицу (матрицу перевозок).

Очевидно, переменные  должны удовлетворять условиям:

(3. )

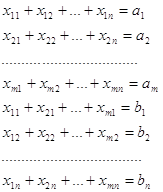
Система (3. ) содержит  уравнений с  неизвестными. Её особенность состоит в том, что коэффициенты при неизвестных всюду равны единице. Кроме того, все уравнения системы (3. ) могут быть разделены на две группы: первая группа из т первых уравнений (“горизонтальные” уравнения) и вторая группа из п остальных уравнений (“вертикальные” уравнения). В каждом из горизонтальных уравнений содержатся неизвестные с одним и тем же первым индексом (они образуют одну строку матрицы перевозок), в каждом из вертикальных уравнений содержатся неизвестные с одним и тем же вторым индексом (они образуют один столбец матрицы перевозок). Таким образом, каждая неизвестная встречается в системе (3. ) дважды: в одном и только одном горизонтальном и в одном и только одном вертикальном уравнениях.

Такая структура системы (3. ) позволяет легко установить ее ранг. Действительно, покажем, что совокупность неизвестных, образующих первую строку и первый столбец матрицы перевозок, можно принять в качестве базиса. При таком выборе базиса, по крайней мере, один из двух их индексов равен единице, а, следовательно, свободные неизвестные определяются условием , .Перепишем систему (3. ) в виде

(3. )

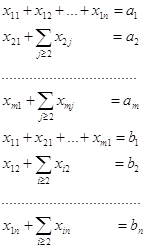
где символы и означают суммирование по соответствующему индексу. Так, например,

При этом легко заметить, что под символами такого суммирования объединяются только свободные неизвестные (здесь , ).

В рассматриваемой нами системе только два уравнения, а именно первое горизонтальное и первое вертикальное, содержат более одного неизвестного из числа выбранных нами для построения базиса. Исключив из первого горизонтального уравнения базисные неизвестные  с помощью вертикальных уравнений, мы получаем уравнение

или короче

(3. )

где символ  означает сумму всех свободных неизвестных. Аналогично, исключив из первого вертикального уравнения базисные неизвестные  с помощью горизонтальных уравнений, мы получаем уравнение

(3. )

Так как для закрытой модели транспортной задачи , то полученные нами уравнения (3. ) и (3. ) одинаковы и, исключив из одного из них неизвестное , мы получим уравнение-тождество 0=0, которое из системы вычеркивается.

Итак, преобразование системы (3. ) свелось к замене двух уравнений (первого горизонтального и первого вертикального) уравнением (3. ). Остальные уравнения остаются неизменными. Система приняла вид

(3. )

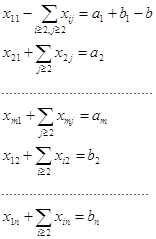
В системе (3. ) выделен указанный выше базис: базисные неизвестные из первых т уравнений образуют первый столбец матрицы перевозок, а базисные неизвестные остальных уравнений образуют первую строку матрицы перевозок без первого неизвестного  [она входит в первое уравнение системы (3. )]. В системе (3. ) имеется  уравнений, выделенный базис содержит  неизвестных, а, следовательно, и ранг системы (3. ) .

Для решения транспортной задачи необходимо кроме запасов и потребностей знать также и тарифы , т. е. стоимость перевозки единицы груза с базы  потребителю .

Совокупность тарифов  также образует матрицу, которую можно объединить с матрицей перевозок и данными о запасах и потребностях в одну таблицу 3.:

Таблица 3. - Совокупность тарифов данные о запасах и потребностях

Пункты Отправления	Пункты назначения									Запасы
						…
						…
						…
…	…			…		…	…			…
						…
Потребности						…				или

Сумма всех затрат, т. е. стоимость реализации данного плана перевозок, является линейной функцией переменных :

(3. )

Требуется в области допустимых решений системы уравнений (3. ) и (3.) найти решение, минимизирующее линейную функцию (3. ).

Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без симплекс-таблиц. Решение можно получить путем некоторых преобразований таблицы перевозок. Эти преобразования соответствуют переходу от одного плана перевозок к другому. Но, как и в общем случае, оптимальное решение ищется среди базисных решений. Следовательно, мы будем иметь дело только с базисными (или опорными) планами. Так как в данном случае ранг системы ограничений-уравнений равен  то среди всех  неизвестных  выделяется  базисных неизвестных, а остальные · неизвестных являются свободными. В базисном решении свободные неизвестные равны нулю. Обычно эти нули в таблицу не вписывают, оставляя соответствующие клетки пустыми. Таким образом, в таблице перевозок, представляющей опорный план, мы имеем  заполненных и · пустых клеток.

На предприятии ОАО «Электросигнал» имеется 4 транзитных склада Аi, на которых хранятся сборочные узлы и 5 цехов Bj, занимающихся сборкой готовой продукции. Ниже, в таблице 3., приведены данные по количеству сборочных узлов на каждом складе, запросы цехов и стоимость перевозки одного агрегата из Аi в Bj. Необходимо составить такой план перевозок, при котором запросы цехов будут удовлетворены при минимальной суммарной стоимости перевозок.

Таблица 3. – Исходные данные по количеству сборочных узлов и стоимость перевозки

Цеха Склад	B1 (b1=40)	B2 (b2=50)	B3 (b3=15)	B4 (b4=75)	B5 (b5=40)
А1 (а1=50)	1,0	2,0	3,0	2,5	3,5
А2(а2=20)	0,4	3,0	1,0	2,0	3,0
А3(а3=75)	0,7	1,0	1,0	0,8	1,5
А4(а4=80)	1,2	2,0	2,0	1,5	2,5

В данном случае Σai=225 >Σbj=220 => имеем дело с открытой моделью транспортной задачи. Сведем ее к закрытой введением фиктивного цеха B6 с потребностью b5=225-220=5 и стоимостью перевозок сi6=0.Имеем таблицу 3. :

Таблица 3. -

Цеха Склад	B1 (b1=40)	B2 (b2=50)	B3 (b3=15)	B4 (b4=75)	B5 (b5=40)	B6 (b6=5)
А1 (а1=50)	1,0	2,0	3,0	2,5	3,5	0
А2(а2=20)	0,4	3,0	1,0	2,0	3,0	0
А3(а3=75)	0,7	1,0	1,0	0,8	1,5	0
А4(а4=80)	1,2	2,0	2,0	1,5	2,5	0

Математическая модель: обозначим xij – количество товара, перевозимого из Аi в Bj. Тогда

x11 x12 x13 x14 x15 x16

x21 x22 x23 x24 x25 x26

X = x31 x32 x33 x34 x35 x36 - матрица перевозок.

x41 x42 x43 x44 x45 x46

min(x11+2x12+3x13+2,5x14+3,5x15+0,4x21+3x22+x23+2x24+3x25+0,7x31+x32+x33+0,8x34+1,5x35++1,2x41+2x42+2x43+1,5x44+2,5x45) (3. )

x11+x12+x13+x14+x15+x16=50

x21+x22+x23+x24+x25+x26=20

x31+x32+x33+x34+x35+x36=75

x41+x42+x43+x44+x45+x46=80

(3. )

 x11+x21+x31+x41=40  

 x12+x22+x32+x42=50

 x13+x23+x33+x43=15

 x14+x24+x34+x44=75

 x15+x25+x35+x45=40

 x16+x26+x36+x46=5

 xij≥0 (i=1,2,3,4 ; j=1,2,3,4,5,6 ) (3. )

Двойственная ЗЛП:

max(50u1+20u2+75u3+80u4+40v1+50v2+15v3+75v4+40v5+5v6) (3. )

	u2+v1≤0,4 u2+v2≤3 u2+v3≤1 u2+v4≤2 u2+v5≤3 u2+v6≤0		u3+v1≤0,7 u3+v2≤1 u3+v3≤1 u3+v4≤0,8 u3+v5≤1,5 u3+v6≤0		u4+v1≤1,2 u4+v2≤2 u4+v3≤2 u4+v4≤1,5 u4+v5≤2,5 u4+v6≤0

u1+v1≤1

u1+v2≤2

u1+v3≤3   (3. )

u1+v4≤2,5

u1+v5≤3,5

u1+v6≤0

ui,vj – произвольные (i=1,2,3,4 ; j=1,2,3,4,5,6 ) 

Будем искать первоначальный план по методу наименьшей стоимости:

1) x21=20 и 2-ую строку исключаем;

2) x31=20 и 1-ый столбец исключаем;

3) x34=55 и 3-ю строку исключаем;

4) x44=20 и 4-ый столбец исключаем;

5) x12=50 и 1-ю строку и 2-ой столбец исключаем и x32=0;

6) x43=150 и 3-ий столбец исключаем;

7) x45=40 и 5-ый столбец исключаем и x46=5.

Составим таблицу 3. . Здесь и далее в нижнем правом углу записываем значение перевозки.

Таблица 3. – Проведение итераций

Цеха Склад	B1 (b1=40)	B2 (b2=50)	B3 (b3=15)	B4 (b4=75)	B5 (b5=40)	B6 (b6=5)
А1 (а1=50)	1,0	50   2,0	3,0	2,5	3,5	0
А2(а2=20)	0,4  20	3,0	1,0	2,0	3,0	0
А3(а3=75)	0,7  20	0   1,0	1,0	55   0,8	1,5	0
5    15   А4(а4=80)	1,2	2,0	2,0	20   1,5	40   2,5	0

Стоимость 1-ого плана:

D1=2•50+0,4•20+0,7•20+0,8•55+2•15+1,5•20+2,5•40=326.

Будем улучшать этот план методом потенциалов: ui- потенциал Аi ,vj- потенциал Bj. Тогда u1+v2=2,u2+v1=0,4, u3+v1=0,7, u3+v2=1, u3+v4=0,8, u4+v3=2, u4+v4=1,5, u4+v5=2,5 ,u4+v6=0.Положим u1=0,тогда v2=2,u3=-1,v1=1,7,v4=1,8, u2=-1,3,u4=-0,3, v3=2,3,v5=2,8,v6=0,3.Составим таблицу 3. :

Таблица 3. - Проведение итераций

Цеха Склад	B1 (b1=40) v1=1,7	B2 (b2=50) v2=2	B3 (b3=15) v3=2,3	B4 (b4=75) v4=1,8	B5 (b5=40) v5=2,8	B6 (b6=5) v6=0,3
0,7   А1 (а1=50) U1=0	0   1,0	- 0,7    50   2,0	- 0,7   3,0	- 0,7   2,5	0,3   3,5	0
0   А2(а2=20) U2=-1,3	- 2,3    20   0,4	0   3,0	- 1,5   1,0	- 1,5   2,0	- 1   3,0	0
0   А3(а3=75) U3=-1	0   0,7  20	0,3    0   1,0	0   1,0	0,3    55   0,8	- 0,7   1,5	0
0,2   А4(а4=80) U4=-0,3	- 0,3   1,2	0   2,0	0    15   2,0	0    20   1,5	0    40   2,5	5   0

В верхнем левом углу здесь и далее записываем значение ui+vj-cij. Имеем: u1+v1--c11 =0,7>0, u1+v6-c16 =0,3>0, u3+v3-c33 =0,3>0, u3+v5-c35 =0,3>0,

u4+v1-c41 =0,2>0. => По критерию оптимальности, первый план не оптимален. Далее max(0,7;0,3;0,3;0,3;0,2)=0,7. => Поместим перевозку в клетку А1В1, сместив 20=min(20,50) по циклу, указанному в таблице штрихом. Получим новую таблицу. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u3+v4=0,8, u4+v3=2, u4+v4=1,5, u4+v5=2,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,8, u3=-1, u4=-0,3,v3=2,3,v5=2,8,v6=0,3. Составим таблицу 3. :

Таблица 3. - Проведение итераций

Цеха Склад	B1 (b1=40) v1=1	B2 (b2=50) v2=2	B3 (b3=15) v3=2,3	B4 (b4=75) v4=1,8	B5 (b5=40) v5=2,8	B6 (b6=5) v6=0,3
0   А1 (а1=50) U1=0	0   1,0  20	- 0,7    30   2,0	- 0,7   3,0	- 0,7   2,5	0,3   3,5	0
0   А2(а2=20) U2=-0,6	- 1,6    20   0,4	0,7   3,0	- 0,8   1,0	- 0,8   2,0	- 0,3   3,0	0
-0,7   А3(а3=75) U3=-1	0   0,7	0,3    20   1,0	0   1,0	0,3    55   0,8	- 0,7   1,5	0
-0,5   А4(а4=80) U4=-0,3	- 0,3   1,2	0   2,0	0    15   2,0	0    20   1,5	0    40   2,5	5   0

Стоимость 2-ого плана:

D2=1•20+2•30+0,4•20+1•20+0,8•55+2•15+1,5•20+2,5•40=312.

Имеем:u1+v6-c16 =0,3>0, u2+v3-c23 =0,7>0, u3+v3-c33 =0,3>0, u3+v5-c35 =0,3>0. => По критерию оптимальности, второй план не оптимален. Далее max(0,3;0,7;0,3;0,3)=0,7 => Поместим перевозку в клетку А2В3, сместив 15=min(20,30,55,15) по циклу, указанному в таблице штрихом. Получим новую таблицу. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u3+v4=0,8, u2+v3=1, u4+v4=1,5, u4+v5=2,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,8, u3=-1, u4=-0,3,v3=1,6, v5=2,8, v6=0,3. Составим таблицу 3.:

Таблица 3. - Проведение итераций

Цеха Склад	B1 (b1=40) v1=1	B2 (b2=50) v2=2	B3 (b3=15) v3=1,6	B4 (b4=75) v4=1,8	B5 (b5=40) v5=2,8	B6 (b6=5) v6=0,3
0   А1 (а1=50) U1=0	0   1,0  35	-1,4    15   2,0	- 0,7   3,0	- 0,7   2,5	0,3   3,5	0
0   А2(а2=20) U2=-0,6	- 1,6    5   0,4	0   3,0	15    - 0,8   1,0	- 0,8   2,0	- 0,3   3,0	0
-0,7   А3(а3=75) U3=-1	0   0,7	-0,4    35   1,0	0   1,0	0,3    40   0,8	- 0,7   1,5	0
-0,5   А4(а4=80) U4=-0,3	- 0,3   1,2	-0,7   2,0	0   2,0	0    35   1,5	0    40   2,5	5   0

Стоимость 3-его плана:

D3=1•35+2•15+0,4•5+1•15+0,8•40+1•35+1,5•35+2,5•40=301,5.

Имеем:u1+v6-c16 =0,3>0,u3+v5-c35 =0,3>0. => По критерию оптимальности, третий план не оптимален. Далее max(0,3;0,3)=0,3. => Поместим перевозку в клетку А3В5, сместив 40=min(40,40) по циклу, указанному в таблице штрихом. Получим новую таблицу. Чтобы 4-ый план был невырожденным, оставим в клетке А4В5 нулевую перевозку. Найдем потенциалы: u1+v1=1,u1+v2=2,u2+v1=0,4,u3+v2=1, u4+v5=2,5, u2+v3=1, u4+v4=1,5, u3+v5=1,5 , u4+v6=0. Положим u1=0,тогда v1=1,u2=-0,6,v2=2,v4=1,5, u3=-1,u4=0, v3=1,6, v5=2,5, v6=0. Составим таблицу 3. :

Таблица 3. - Проведение итераций

Цеха Склад	B1 (b1=40) v1=1	B2 (b2=50) v2=2	B3 (b3=15) v3=1,6	B4 (b4=75) v4=1,5	B5 (b5=40) v5=2,5	B6 (b6=5) v6=0
0   А1 (а1=50) U1=0	0   1,0  35	- 1,4    15   2,0	- 1   3,0	- 1   2,5	0   3,5	0
0   А2(а2=20) U2=-0,6	- 1,6    5   0,4	0   3,0	15    - 1,1   1,0	- 1,1   2,0	- 0,6   3,0	0
-0,7   А3(а3=75) U3=-1	0   0,7	-0,4    35   1,0	-0,3   1,0	0   0,8	40    - 1   1,5	0
-0,2   А4(а4=80) U4=0	0   1,2	-0,4   2,0	0   2,0	0    75   1,5	0    0   2,5	5   0

Стоимость 4-ого плана:

D4=1•35+2•15+0,4•5+1•15+1•35+1,5•40+1,5•75=289,5.

Для всех клеток последней таблицы выполнены условия оптимальности:

1) ui+vj-сij=0 для клеток, занятых перевозками;

2) ui+vj-сij ≤0 для свободных клеток.

Несодержательные ответы:

Прямой ЗЛП:

 35 15 0 0 0 0

 5 0 15 0 0 0

 X = 0 35 0 0 40 0

 0 0 0 75 0 5

 min=289,5.

Двойственной ЗЛП:

U1=0 ; U2=-0,6 ; U3=-1 ; U4=0 ; V1=1 ; V2=2 ; V3=1,6 ; V4=1,5 ; V5=2,5 ; V6=0.

max=289,5.

Так как min=max, то по критерию оптимальности найдены оптимальные решения прямой и двойственной ЗЛП. Содержательный ответ: Оптимально перевозить так:

Из А1 в B1 – 35 сборочных агрегатов;

Из А1 в B2 – 15 сборочных агрегатов;

Из А2 в B1 – 5 сборочных агрегатов;

Из А2 в B3 – 15 сборочных агрегатов;

Из А3 в B2 – 35 сборочных агрегатов;

Из А3 в B5 – 40 сборочных агрегатов;

Из А4 в B4 – 75 сборочных агрегатов.

При этом стоимость минимальна и составит Dmin=289,5. 5 сборочных агрегатов необходимо оставить на складе А4 для их последующей перевозки в другие Цеха.

Список использованной литературы

1. Е.Г. Гольштейн, Д.Б. Юдин «Задачи линейного программирования транспортного типа», Москва, 2007.

2. И.Л. Акулич, В.Ф. Стрельчонок «Математические методы и компьютерные технологии решения оптимизационных задач», Рига, 2006.

3. Астафуров В.Г., Колодникова Н. - Компьютерное учебное пособие, раздел “Анализ на чувствительность с помощью двойственной задачи”, Томск-2004.

4. Алесинская Т.В. - Задачи по исследованию операций с решениями. Москва, 2008.

5. Смородинский С.С., Батин Н.В. - Оптимизация решений на основе методов и моделей математического программирования: Учебное пособие. Воронеж, 2009