Контрольная работа: Статистические расчеты средних показателей

Контрольная работа: Статистические расчеты средних показателей

Министерство образования и науки Украины

Национальный горный университет

            Институт заочно – дистанционного образования

Кафедра экономической  кибернетики

и информационных технологий

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Статистика»

          Специальность      7.050104 «Финансы»

          Группа                                 Б-Ф-06

Студентка             Вознюк Е.О

Этап	Время	Отметка о выполнении
получение задания
сдача отчета

«Задание проверил» доц., к. т. н.                               Демиденко М.А.

«Задание выполнила»                                                                 Вознюк Е.О

 

г. Днепропетровск 2007г.

Задача 1.

В табл.1 представлен интервальный вариационный ряд распределения средних месячных доходов в группе из 123 служащих банка:

Интервалы доходов, грн./мес.	Число служащих
530-930	6
930-1330	9
1330-1730	15
1730-2130	28
2130-2530	29
2530-2930	23
2930-3330	13

Вычислить:

1.         Средний доход  и  дисперсию.

2.         Вычислить моду и медиану доходов.

3.         Представить вариационный ряд графически полигоном, гистограммой, кумулятой.

4.         Сформулировать выводы по результатам расчетов.

Решение.

1. Для расчета среднего дохода и дисперсии составим таблицу:

Интервалы доходов, грн./мес.	Число служащих, f	Середина интервала, xi	xi* mi		Накопленная частота
530-930	6	730	4380	11842094	6
930-1330	9	1130	10170	9088019	15
1330-1730	15	1530	22950	5488162	30
1730-2130	28	1930	54040	1175300	58
2130-2530	29	2330	67570	1104105	87
2530-2930	23	2730	62790	8145913	110
2930-3330	13	3130	40690	12873480	123
Итого	123		262590	49717073

Средняя зарплата рабочего: 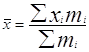= 262590/123= 2134.88 грн./мес.;

Дисперсия зарплаты 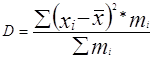= 49717073/123= 404203.85

2. Модальный интервал [2130-2530], т.к. частота этого интервала наибольшая (f=28). Мода:

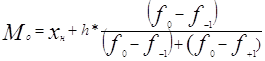=2130+400*(29-28)/(29-28+29-23)= 2187.14 грн./мес.

3.         Медианный интервал [2130-2530], т.к. признак под номером (123+1)/2=62 находится в указанном интервале. Медиана 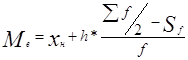=2130+400*(123/2-58)/29=2178.28 грн./мес.

4.         Представим вариационный ряд графически полигоном, гистограммой, кумулятой:

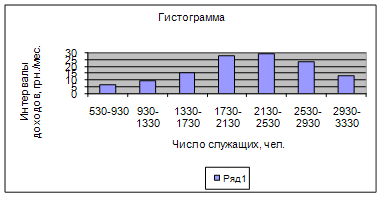
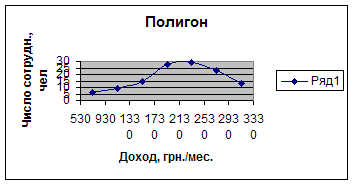
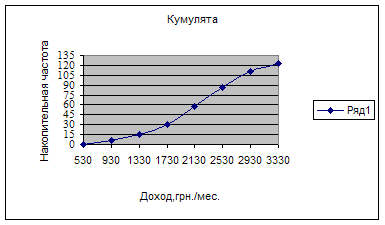
Выводы: средний доход составляет 2134.88 грн./мес., а дисперсия – 404203.85. Самый распространенный доход 1907,78 грн./мес. Половина служащих получает зарплату менее 2178.28 грн./мес., а половина – меньше 2178,28 грн./мес.

Задача 2.

В табл.2 приведен ряд динамики помесячного оборота отделения банка.

Месяц	Условное время, t	Товарооборот, уi, тыс.грн.
Январь	1	6503
Февраль	2	6703
Март	3	6903
Апрель	4	7623
Май	5	7003
Июнь	6	7403
Июль	7	7683
Август	8	7803
Сентябрь	9	8003
Октябрь	10	8103
Ноябрь	11	8153
Декабрь	12	8203
Итого	78	90086

Рассчитать:

1.         Средний месячный оборот отделения банка.

2.         Абсолютный прирост оборота.

3.         Коэффициенты и темпы роста и прироста оборота.

4.         Средний абсолютный прирост.

5.         Средний темп роста.

6.         Изобразить ряд динамики графически.

7.         Выровнять ряд динамики с помощью линейной модели парной регрессии.

8.         Сформулировать выводы по результатам расчетов.

Решение.

1.         Средний месячный оборот отделения банка: 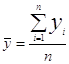=90086/12 =

= 7507.17 тыс.грн.

где yi – уровни ряда динамики.

2-3. Формулы для расчета

- базисного и цепного абсолютного прироста

,             ;

- базисного и цепного коэффициента роста

,             ;

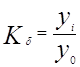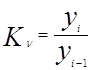- базисного и цепного темпа роста

,      ;

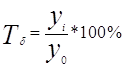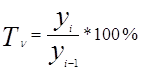- базисного и цепного коэффициента прироста

,            ;

- базисного и цепного темпа прироста

,            ;

-     среднего абсолютного прироста

,

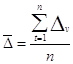где n – число цепных абсолютных приростов

-     среднегодового темпа роста

,

где n – число цепных коэффициентов роста;

Результаты расчетов приведены в таблице:

Условное время, t	Оборот, тыс.грн.	Абсолютный прирост		Коэф. роста		Темп роста, %		Коэф. прироста		Темп прироста, %
		цепной	базисный	цепной	базисный	цепной	базисный	цепной	базисный	цепной	базисный
1	6503	-	-	-	-	-	-	-	-	-	-
2	6703	200	200	1,03	1,03	103,13	103,13	0,03	0,03	3,13	3,13
3	6903	200	400	1,03	1,06	103,03	106,25	0,03	0,06	3,03	6,25
4	7623	720	1120	1,11	1,18	110,59	117,50	0,11	0,18	10,59	17,50
5	7003	-620	500	0,92	1,08	91,76	107,81	-0,08	0,08	-8,24	7,81
6	7403	400	900	1,06	1,14	105,80	114,06	0,06	0,14	5,80	14,06
7	7683	280	1180	1,04	1,18	103,84	118,44	0,04	0,18	3,84	18,44
8	7803	120	1300	1,02	1,20	101,58	120,31	0,02	0,20	1,58	20,31
9	8003	200	1500	1,03	1,23	102,60	123,44	0,03	0,23	2,60	23,44
10	8103	100	1600	1,01	1,25	101,27	125,00	0,01	0,25	1,27	25,00
11	8153	50	1650	1,01	1,26	100,63	125,78	0,01	0,26	0,63	25,78
12	8203	50	1700	1,01	1,27	100,62	126,56	0,01	0,27	0,62	26,56

4. Средний абсолютный прирост 1700/11=154,55 тыс.грн.

5.         Средний темп роста: =102,2%.

Выводы: за отчетный период оборот увеличился на 1700 тыс.грн. или 26,56%. Наибольший прирост оборота (на 10,59% или 720 тыс.грн.) наблюдался в апреле, а наибольшее падение оборота (8,24% или 620 тыс.грн.) наблюдалось в мае. В среднем за месяц оборот увеличивался на 2,2% или 154,55 тыс.грн.

6.         Изобразитм ряд динамики графически:

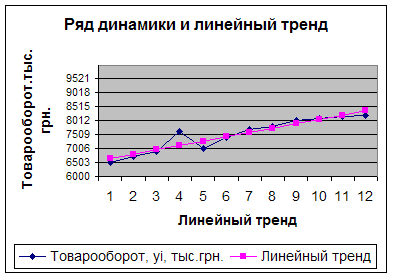
7. Выполним выравнивание ряда динамики с помощью линейной модели парной регрессии.

При выравнивании по линейной модели необходимо вычислить коэффициенты линейного уравнения .

Значения коэффициентов рассчитываются по формулам:

,   

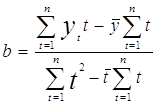где ,  -  средние значения у и t.

Для расчета коэффициентов уравнения составим таблицу

	Условное время, t	Товарооборот, уi, тыс.грн.	y*t	t2
	1	6503	6503	1	6646,974
	2	6703	13406	4	6803,373
	3	6903	20709	9	6959,772
	4	7623	30492	16	7116,17
	5	7003	35015	25	7272,569
	6	7403	44418	36	7428,967
	7	7683	53781	49	7585,366
	8	7803	62424	64	7741,765
	9	8003	72027	81	7898,163
	10	8103	81030	100	8054,562
	11	8153	89683	121	8210,96
	12	8203	98436	144	8367,359
Сумма	78	90086	607924	650	90086
Сред.знач.	6,5	7507.166	50660.33	54,16667	7507.166

b=(607924 -7507,166*78)/(650-6,5*78)=156,4;

а=7507,16- 156.4*6,5=6490.57, т.е. уравнение имеет вид у=6490.57+156,4*t.

По полученному уравнению рассчитаем теоретические значения товарооборота (см. таблицу выше).

Вывод: результаты выравнивания свидетельствуют о тенденции товарооборота к увеличению, т.к. b>0.

Задача 3.

В табл. 3 приведены сведения о количестве приобретенных продуктов питания на душу населения в ценах ноября и декабря текущего года:

Продукты	ноябрь		декабрь
	Кол-во, кг	Цена, грн./кг	Кол-во, кг	Цена, грн./кг
Мясные продукты	6,2	20,4	4,5	22,4
Рыбные продукты	18	8,4	15	9,4
Овощи и фрукты	8	1.9	9,5	1,4
Хлебобулочные	12	1,4	15	1,5

Вычислить:

1.         Общий индекс динамики затрат на продукты питания.

2.         Агрегатные индексы Э.Ласпейреса и Г.Пааше динамики затрат на продукты питания.

3.         Абсолютное изменение общих затрат, а также изменение затрат из-за изменения цен и из-за изменения количества продуктов.

4.         Сформулировать выводы по рассчитанным коэффициентам.

Решение.

Составим вспомогательную таблицу

Продукты	апрель		май		q0* p0	q1*p1	q1*p0	q0*p1
	Кол-во, q0, кг	Цена, p0, грн./кг	Кол-во, q1, кг	Цена, p1, грн./кг
Мясные продукты	6,2	20,4	4,5	22,4	126,48	100,8	91,8	138,88
Рыбные продукты	18	8,4	15	9,4	151,2	141	126	169,2
Овощи и фрукты	8	1.9	9,5	1,4	15,2	13,3	18,05	11,2
Хлебобулочные	12	1,4	15	1,5	16,8	22,5	21	18
Сумма					309,68	277,6	256,85	337,28

1.         Общий индекс динамики затрат на питание:

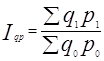=277,6/309.68 =0.896409 или 89.64%.

Вывод: в общем затраты на питание уменьшились на 10.36 %.

2.   Агрегатные индексы Э.Ласпейреса:

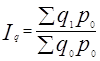=256,85/309,68=0,8294 или 82.94%

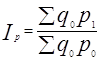=337.28/309.68=1,089124 или 108,91 %

Выводы: за счет уменьшения количества приобретаемых продуктов общие затраты уменьшились на 17.06 %, а за счет роста цен общие затраты увеличились на 8,91 %.

Агрегатные индексы Г.Пааше:

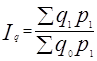=277.60/337.28=0,823055 или 82.31 %

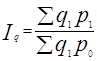=277.60/256.85=1,080786 или 108.08 %

Выводы: за счет уменьшения количества приобретаемых продуктов общие затраты уменьшились на 17.69 %, а за счет роста цен общие затраты увеличились на 8.91 %.

3.   Абсолютное изменение общих затрат:

=277.60-309.68 =-32,08 грн.

4.   Абсолютное изменение затрат из-за изменения количества продуктов:

=256.85-309.68 =-52,83 грн.

5.   Абсолютное изменение затрат из-за изменения цен:

=277.60-256.85=20,75 грн.

Выводы: в общем затраты на питание уменьшились на 32,08 грн. При этом за счет уменьшения количества приобретаемых продуктов общие затраты уменьшились на 52,83 грн., а за счет роста цен общие затраты увеличились на 20,75 грн.

Задача 4.

В банке работают 3 бригады кассиров. В таблице приведены сведения о численности и средней заработной плате работников каждой бригады в первом и втором кварталах текущего года.

Бригады	1-й квартал		2-й квартал
	Ч0, чел.	ЗП0, грн.	Ч1, чел.	ЗП1, грн.
1	15	443	20	473
2	20	503	20	513
3	25	283	30	293

Вычислить:

1.         Среднюю зарплату кассиров по банку.

2.         Для средней зарплаты по банку вычислить индексы динамики переменного состава, фиксированного состава и структурных сдвигов.

3.         Рассчитать общее изменение средней зарплаты, а также ее изменение, обусловленное изменением зарплаты в бригадах, и изменение, вызванное сдвигами в структуре численности.

4.         Сформулировать выводы по результатам расчетов.

Решение.

Составим вспомогательную таблицу

Бригады	1-й квартал		2-й квартал		f0*x0	f1*x1	f1*x0
	f0, чел.	x0, грн.	f1, чел.	x1, грн.
1	15	443	20	473	6645	9460	8860
2	20	503	20	513	10060	10260	10060
3	25	283	30	293	7075	8790	8490
Сумма	60		70		23780	28510	27410

1.   Средняя зарплата кассиров по банку:

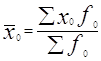=23780/60=396,33 грн.

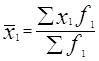=28510/70=407.29 грн.

2.   Индекс переменного состава:

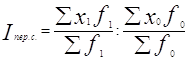=407,29/396,33=1,02765 или 102,8 %.

Индекс фиксированного состава:

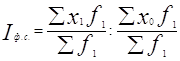=(28510/70)/(27410/70)=1,04014 или 104,01 %.

3.   Индекс структурных сдвигов:

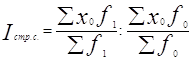=(27410/70)/(23780/60)=0,987989 или 98,80 %.

4.   Общее изменение средней зарплаты:

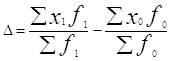=407,29-396,33=10,96 грн.

5.   Изменение средней зарплаты за счет изменения зарплаты в бригадах:

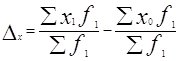=28510/70-27410/70=15,72 грн.

6.   Изменение средней зарплаты за  счет сдвигов в структуре численности:

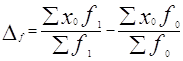=27410/70-2378010/60=-4,76 грн.

Вывод: в целом средняя зарплата во втором квартале больше, чем в первом на 10,96 грн. или 2,8%. Из-за роста зарплаты в каждом цехе средняя зарплата увеличилась на 15,72 грн. или 4,01 %, а из-за сдвигов в структуре численности средняя зарплата уменьшилась на 4,76 грн. или 1,26%.

Литература:

1.         Статистика: Підручник/А.В.Головач, А.М.Єріна, О.В.Козирєв та ін. – К.:Вища шк.., 1993.

2.         Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория татистики: Учебник. – М.: ИНФРА-М, 1998. – 416 с.