- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Курсовая работа: Дифференциальное исчислениеКурсовая работа: Дифференциальное исчислениеМинистерство науки и образования Кафедра "ИиВТ" ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К курсовой работе По предмету: Высшая математика На тему: Дифференциальное исчисление г. Талдыкорган 2008 год Введение 1. Предмет математики и основные периоды ее развития. Математика представляет собой один из самых важных фундаментальных наук. Слово "математика" произошло от греческого слова "матема", что означает знания. Возникла математика на первых же этапах человеческого развития в связи с практической деятельностью людей. С самых древних времен люди, производя различные работы, встречались с необходимостью выделения и образования тех или иных совокупностей объектов, участков земли, жилищных потребностей объектов, жилищных помещений. Во-первых, во всех этих случаях нужно было устанавливать количественные оценки рассматриваемых множеств, измерять их площади и объемы, сравнивать, вычислять, преобразовывать. По определению, данному Ф.Энгельсом: МАТЕМАТИКА – это наука изучает количественные отношения и пространственные формы реального мира. 2. Основные математические понятия, такие как число, геометрическая фигура, функция, производная, интеграл, случайное событие и его вероятность и т.д. За свою историю математика, которая развивалась в тесной связи с развитием производственной деятельностью людей и общественной культуры, превратилась в стройную дедуктивную науку, представленную как мощный аппарат для изучения окружающего нас мира. Академик А.Н. Калинов выделил четыре основных развития в истории математики. Первый – период зарождения математики, начало которого лежит и теряется в глубинах тысячелетий истории человечества и продолжается до VI – V веков до нашей эры. В этом периоде создается арифметика, а также зачатки геометрии. Математические сведения этого периода состоят в основном из свода правил решения различных практических задач. Второй период – элементарной математики, т.е. математики, постоянных величин (VI – V вв. до н.э. – XVII в. н.э.). Уже в начале этого периода (около 300 лет до н.э.) Евклид создает теорию трех книг ("Начало Евклида" - первый из дошедших до нас больших теоретических исследований по математике), в которых, в частности изучается дедуктивным образом на базе система аксиомы вся элементарная геометрия. Изданной в IX веке сочинения ал-Хорезми "Кибат ал-Джарап ал-Мукабана" содержит общие приемы решения задач, сводящие к управлению первой и второй степени. В XV веке вместо громких выражений стали употреблять знаки + и -, знаки степеней, корней, скобки. В XVI веке Ф.Виет применяет буквы для обозначения данных и не известных величин. К середине XVII века в основном сложилась современная алгебраическая символика, и этим были созданы основы формального математического языка. Третий период – период создания математики переменных величин (XVII век – середина XIX века). Начиная с XVII века, в связи с изучением количественного отношения в процессе их изменения, на первый план выносили понятия переменной величины и функции. В этом периоде в работах Р.Декарта на базе мирового исследования метода системных координат создается аналитическая геометрия. В ра ботах И.Ньютона и Г.В.Лейбница завершает создание дифференциального интегрального исчисления. Четвертый период – современные математики. Его начало следует относить к двадцатым годам XIX века – этот период начинается с работ Э.Гаусса, в которых заложены идеи теории алгебраических структур, В.И.Лобачевского, который открыл первую неевклидовую геометрию – геометрию Лобачевского. В последствии дальнейшего распространения получил аксиоматический метод, в новую фазу вступили работы по обоснованию математики, математической логики и математическому моделированию. Создание в середине прошлого века ЭВМ привело не только более к глубокому и широкому применению математики в других областях знания, в технических науках, в вопросах организации и управления производством, но и зарождению развития новых областей теоретических и прикладных математических функций. Проникновения методов современной математики и ЭВМ в другие наук и практику применяет на столько всеобщий и глубокий характер, что одно из способностей нынешнего этапа развития человеческой культуры считается процесс математизации знаний и компьютеризации всех сфер трудовой деятельности и жизни людей. 3. Понятие о математическом моделировании. При изучении количественных характеристик сложных объектов, процессов явлений, пользуются методом математического моделирования, который состоит в том, что рассматриваемые закономерности формируются на математическом языке и исследуются при помощи соответствующих математических средств. Математический модуль изучаемого объекта записывается при помощи математических символов и состоит из совокупности уравнений, неравенств, формул, алгоритмов программ (для ЭВМ), в состав которых входят переменные и постоянные величины, различные операции, функции, быть может, и их производные, и другие математические понятия. Приемами составления простейших математических моделей служит хорошо известный, из курса математики средней школы, прием решения задач при помощи уравнений и систем уравнений – полученное уравнение или система уравнений является математической моделью данной задачи. Это были примеры задач с единственным решением – детерминированных задач. Однако часто встречаются задачи, имеющие много решений. В таких случаях на практике возникает вопрос о нахождении такого решения, которое является наиболее подходящим для той или иной точки зрения. Такие решения называются оптимальными решениями. Оптимальное решение определяется как решение, для которого некоторая функция называется целевой функцией, принимает при заданных ограничениях наибольшее и наименьшее значения. Целевую функцию составляют из условия задачи, и она выражает величину, которую нужно оптимизировать (т.е. максимизировать или минимизировать), - например, получаемую прибыль, расходы, ресурсы и т.п. Оказывается, что широкий класс, в частности задачи управления, составляют задачи в математических моделях которых условия на переменных создают неравенство или равенство. Теория и методы решения таких задач составляет раздел математики, известный под названием "Математическое программирование". Если ограничения и целевая функция является многочисленным первой степени (линейны), то такие задачи составляют раздел математического программирования. Математические модели больших производных систем, как правило, имеют сложную структуру. В частности, в них количество переменных и неравенств или уравнений могут насчитывать несколько десятков и даже сотен степеней имеют довольно сложный вид. Такие задачи решаются в вычислительных центрах с использованием больших вычислительных машин. Следуя А.Н.Тихонову, в процессе решения реальных задач методом математического моделирования вычисляем следующие пять этапов: 1. Построение качественной модели, т.е. рассматривание явлений, выделение основных факторов и установление закономерностей, которые имеют место в следующем явлении. 2. Построение математической модели, т.е. перевод на язык математических состояний, установленных качественных закономерностей явлений. На этом же этапе состояния целевая функция, т.е. такая числовая характеристика переменных, наибольшему или наименьшему значению которой соответствует лучшая ситуация с точки зрения предыдущего решения. 3. Решение получаемой задачи. В связи с тем, что часто математические модели являются довольно громадными, вычисления проводятся с помощью ЭВМ в вычислительных центрах. 4. Сопоставление результатов вычислений являются неудовлетворительными, то переходят ко второму циклу процесса моделирования, т.е. повторяют этапы 1, 2, 3 с должными уточнениями информации пока не будет достигнуто удовлетворительное соглашение с имеющимися данными о модулируемом объекте. Математические методы необходимо применять при решении крупных задач, таких как: финансовые отношения, планирование народного хозяйства, использование атомной энергией в широких целях, создание больших воздушных и космических кораблей разного назначения, обеспечение длительной работы научных экспедиций в космосе и т.д. Однако было бы ошибочно думать, что математические методы нужны только для решения крупных задач. При изучении наук в средней школе мы встречаемся с применениями математических методов и вычислений в решении конкретных различных задач. Подобные задачи встречаются в ежедневной работе технических специалистов, экономистов, технологов. Поэтому работникам народного хозяйства, в какой бы области они не трудились, необходимо владеть основными методами исследования и приемами вычисления, устным, письменным, и машинным счетам. Специалисты должны иметь полное представление о возможностях современной ЭВМ. В средней школе мы ознакомились с основными теориями уравнений, их систем, векторов, дифференциального и интегрального исчислениями и их применениями в решении практических задач. Цель изучения математики в средних специальных заведениях состоит в том, чтобы углубить знания по изученным разделам и ознакомиться с некоторыми новыми разделами математики (аналитической геометрией, теорией вероятности и др.), которые обогащают общую культуру, развивает логическое мышление, широко используется в математическом моделировании задач, с которыми встречается современный специалист в своей повседневной деятельности. Типовой учебный план Типовой учебный план – это документ, предназначенный для реализации государственных требований к минимуму содержания и уровня подготовки выпускных учебных заведений средне специального образования. Он определяет общий перечень дисциплин, и обязательные объемы времени для их реализации, виды и минимальную продолжительность произведенной практики, примерный перечень учебных кабинетов, лабораторий и мастерских. В учебном плане также предусматривается курсовое проектирование не более чем по трем дисциплинам во весь период обучения. Виды производственной практики и их продолжительность определяется в соответствии с типовой учебной практики по заданной специальности. График учебного процесса носит рекомендательный характер и может быть откорректирован учебным заведением при обязательном соблюдении продолжительности теоретического обучения, экзаменационных сессий, а также сроков проведения зимних и завершающих учебный год летних каникул (см. таблицу 1). ТАБЛИЦА 1
Из учебного плана видно, что на предмет "Высшая математика" всего отводится 91 час. Из них 35 – теоретических, 13 – практических, 13 часов отводится на лабораторные занятия и 30 часов отведено на курсовой проект. Минимальное количество контрольных работ составляет 1 работа. Зачета нет. Курсовой проект сдается в 7 семестре. Экзамен проводится в 7 семестре. Предмет "Высшая математика" изучается на 3 курсе. В 7 семестре обучения 13 недель, в неделю по 7 часов: 13*7=91 час. Предмет полностью изучается на 3 курсе в 7 семестре. Тематический план Тематический план – является частью учебной программы. Учебная программа - это документ, в котором дается характеристика содержания изучаемого материала по годам обучения и разделам (темам). Тематический план состоит из разделов, в которые входят темы. Тематический план распределяет часы по разделам из общего количества часов. В тематическом плане по предмету "Высшая математика" в разделе "Дифференциальное исчисление" отводится 36 часов. ТАБЛИЦА 2
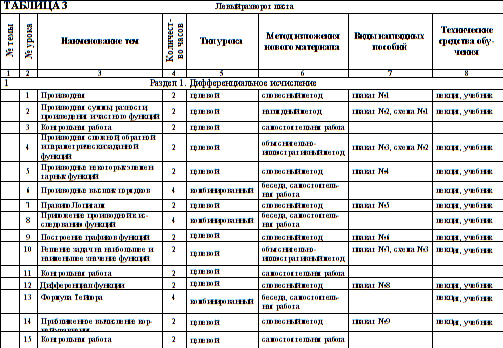
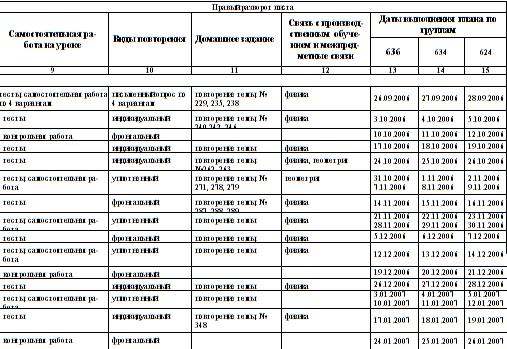
На изучение раздела "Дифференциальное исчисление" в предмете "Высшая математика", дается 36 часов. Из них: 22 часа теоретических занятий и 14 часов посвящены практическому изучению. Календарно-тематический план Календарно-тематический план – планирующее учетный документ, его целями является определение тематики, тип метода и оснащение уроков по выбранному предмету. Составление календарно-тематического плана является первым шагом создания поурочной систематизации. Исходным документом здесь является учебная программа. Календарно тематический план предусматривает межпредметные связи. При соответствии календарно-тематического плана учебной программе ориентируются на тематический план при составлении поурочного плана. Календарно-тематический план (см. таблицу 3).
Разработка урока Изучая учебную программу, преподаватель внимательно анализирует каждую тему, что дает возможность четко определить содержание обучения, установить межпредметные связи. На основе учебной программы составляется календарно-тематический план и уже на основе календарно-тематического плана составляется поурочный план. При определении цели и содержания урока, вытекающей из учебной программы, определяется содержание записи, умений и навыков, которые учащиеся должны усвоить на данном уроке. Анализируя предыдущие уроки, и устанавливая в какой мере решены их задачи, выясняют причину недочетов, и на основе этого определяют какие изменения необходимо внести в проведения данного урока. Намечают структуру урока и время на каждую ее часть, формируют содержание и характер воспитательной работы во время урока. План урока Предмет: Высшая математика Группа 636 Тема: Производная Цели: а) обучающая: Познакомить учащихся с понятием производная, рассказать о ее свойства и методы нахождения б) развивающая: Развить интерес к решению задач по данной теме в) воспитательная: Выработать потребность в самообразовании Тип урока: целевой Метод изложения: словесный Наглядные пособия: плакат Время: 90 мин. Ход урока I. Вводная часть: 1. Организационный момент: проверка по рапортичке время 2 мин. 2. Проверка домашнего задания: время 15 мин. Тест (приложение 1) II. Основная часть: 1. Сообщение цели новой темы 2. Изложение нового материала время 40 мин. а) Задачи, приводящие к понятию производной б) Производная функции в) Физический и геометрический смысл производной г) Вычисление производной на основе ее определения д) Дифференцируемость непрерывной функции 3. Ответы на вопросы учащихся время 10 мин. 4. Закрепление нового материала время 20 мин. Самостоятельная работа по 4 вариантам (приложение 2) III. Заключительная часть: время 3 мин. 1. Подведение итогов 2. Задание на дом: повторение темы, № 229, 235, 238 3. Заключительное слово преподавателя Преподаватель:___________________________ Список литературы 1. Г.Л. Луканкин, Н.Н. Мартынов "Высшая математика", Москва "Просвещение" 1988 год 2. Ю.К. Бабанский "Высшая математика", Москва "Просвещение" 1988 год 3. Ю.К. Бабанский "Высшая математика", Москва "Просвещение" 1983 год 4. И.Н. Бронштейн, К.А. Семендяев "Справочник по математике", Москва "Просвещение" 1990 год Приложение 1 ТЕСТ 1. Найдите предел а) 9 б) в) -9 г) -8 2. Вычислите предел а) 5 б) -1 в) -5 г) - 3. Вычислите предел а) cos б) в) г) 4. Вычислите предел а) -2 б) в) г) 2 5. Вычислите предел а) -1 б) 2 в) -5 г) 1 Правильный ответ г) Приложение 2 САМОСТОЯТЕЛЬНАЯ РАБОТА 1. Найти мгновенную скорость в момент времени t0 свободного падения тела в поле тяжести Земли (I, II, III, IV). 2. Точка движется
прямолинейно по закону x(t) = V0t + I в.: при t = 0 II в.: в момент t0 III в.: при t = 7 IVв.: в момент времени t = 7c 3. Найдите производную функции: I в.: f(x) = x2 II в.: f(x) = 2x3 + 4x + 4 III в.: f(x) = IVв.: f(x) = 3x2 + 4 4. Найдите производную функций в точках x = 1, x = 3. I в.: f(x) = II в.: f(x) = (x + 5)2 III в.: f(x) = 4 – x3 IVв.: f(x) = 5x4 + 2x3 – 3x + 6 5. Найдите производную функций в данных точках. I в.: f(x) = cos x, при х = II в.: f(x) = tg x, при х = III в.: f(x) =cos 2x, при х = IVв.: f(x) = x2 + 4x + 72, при х = -5 Приложение 3 Конспект урока на тему "Производная" 1. Задачи, приводящие к понятию производной. Рассмотрим движение материальной точки М вдоль оси Ох (рис.1). За начало отсчета (точка О) примем положение материальной точки в момент времени t = 0. Пусть в момент времени t координата движущейся точки х равна f(t), т.е. координата х материальной точки есть функция времени:
Х = f(t), t Є [0; T] О М х Эта функция называется законом движения, задается формулой: X = Vt На практике поезда, автомобили движутся равномерно и прямолинейно лишь на некоторых участках, а в общем случае их движение неравномерное. При неравномерном прямолинейном движении материальная точка за разные, но равные по длительности промежутки времени может совершать разные как по времени, так и по направлению перемещения. Для неравномерного движения вводится понятие средней скорости Vср, которая зависит от выбора моментов времени t0 и t1: Vср (t1, t0) = Проиллюстрируем сказанное
примером. Из курса физики известно, что свободное падение тел в поле тяжести Земли
является неравномерным движением и совершается по закону х = Vср(1, 0) = в то время как для второй секунды движения (t1 = 2, t0 = 1) она уже равна в три раза большему значению: Vср(2, 1) = Средняя скорость не может полностью характеризовать неравномерное движение. Для полной характеристики вводят так называемую мгновенную скорость. Очевидно, что средняя скорость Vср (t1, t0) тем полнее характеризует движение за промежуток времени от t0 до t1, чем меньше длительность этого промежутка. Предел средней скорости за промежуток времени от t0 до t1 при t1, стремящимся к t0, называется мгновенной скоростью V(t0) в момент времени t0, т.е.:
2. Производная функции В рассмотренных выше задачах различные физические величины вводились с помощью некоторого предела одного и того же вида. Поэтому имеет смысл рассмотреть предел для функции в общем случае. Определение. Пусть задана функция f(x), x Є(a; b), и пусть х0 – некоторая точка интервала (a; b). Предел f ′ (x0) = Функция, имеющая производную в некоторой точке, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием и обозначается с помощью штриха. Если ввести приращение
аргумента f ′ (x0) = Часто для обозначения
производной вместо штриха используется символ Так как х0 – произвольное значение аргумента, то будем обозначать его просто Х. Тогда: f ′ (x) = Возвращаясь к рассмотренным выше задачам, можем теперь сказать, что искомые величина мгновенной скорости движения V(t) является производной от соответствующей функции: V(t) = x ′ (t) 3. Физический и геометрический смысл производной. Дадим геометрическое
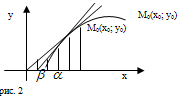
истолкование производной. Пусть кривая К является графиком непрерывной функции
у = f(x), x Є [a; b] (рис. 2). На кривой К рассмотрим точки М0(х0;
у0) и М1(х1; у1) и проведем секущую
М0М1. Ее угловой коэффициент k = tg
Пусть теперь ) Если функция f(x) дифференцируема в точке х0, то существует предел:
и следовательно, существует прямая М0Т, являющаяся предельным положением секущей при приближении точки М1 по кривой к М0. Эта прямая называется касательной к кривой К в точке М0. Таким образом, если
функция у = f(x) дифференцируема в точке х0, то ее график имеет
касательную в точке М0(х0; f(x0)), угловой коэффициент которой равен
4. Вычисление производной на основе ее определения. Исходя из определения производной сформулируем следующее правило нахождения производной функции в точке: Чтобы вычислить производную функции f(x) в точке x0 нужно: 1) Найти f(x) - f(x0); 2) составить разностное
отношение 3) вычислить предел
разностного отношения при
5. Непрерывность дифференцируемой функции. Сформулируем и докажем необходимое условие существования производной. Теорема: Если функция f(x) имеет производную в точке x0, то она непрерывна в этой точке. Согласно условию теоремы функция f(x) в точке x0 дифференцируема, т.е. существует предел:
Используя свойство предела, запишем это равенство в следующем виде:
где
где
Последнее означает непрерывность функции f(x) в точке x0. Замечание. Из доказанной теоремы легко усмотреть, что если функция не является непрерывной в некоторой точке, то она в этой точке не имеет производной. Таким образом непрерывность в точке – необходимое условие дифференцируемости в точке. Далее заметим, что непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, т.е. из непрерывности функции в точке не следует ее дифференцируемость в этой точке. Методика проведения урока. Захожу в кабинет, здороваюсь с учащимися. Начинается вводная часть урока. I. Вводная часть: 1. Организационный момент: проверка по рапортичке время 2 мин. Проверяю наличие учащихся по рапортичке. На проверку наличия учащихся на уроке отвожу 2 минуты. Затем делаю опрос домашнего задания. 2. Проверка домашнего задания: время 15 мин. Тест Опрос провожу в виде теста из 5 вопросов. В тест включаю вопросы по пройденной теме. На тест отвожу 15 минут. ТЕСТ 1. Найдите предел а) 9 б) в) -9 г) -8 2. Вычислите предел а) 5 б) -1 в) -5 г) - 3. Вычислите предел а) cos б) в) г) 4. Вычислите предел а) -2 б) в) г) 2 Правильный ответ г) 5. Вычислите предел а) -1 б) 2 в) -5 г) 1 Правильный ответ Г. В результате теста, я смогу определить, как был усвоен материал, данный на предыдущем уроке. Сделаю выводы: а) правильно ли был подобран тип урока и метод изложения нового материала; б) правильно ли был преподнесен материал; в) выявлю пробелы в знаниях по пройденной теме; г) выявлю учеников, которым был не доступен материал и позанимаюсь с ним на дополнительном уроке; д) выявлю учеников, которым можно давать опережающие задания для их самообразования; е) исправлю ошибки в проведении урока, выясненные при тестировании класса. Перехожу к основной части урока.Где сообщаю цели новой темы. Излагаю новый материал. Отвечаю на вопросы учащихся. Закрепляем пройденный материал самостоятельной работой по 4 вариантам. На основную часть отделяю 70 минут. II. Основная часть: 1. Сообщение цели новой темы 2. Изложение нового материала время 40 мин. а) Задачи, приводящие к понятию производной Из курса физики известно,
что свободное падение тел в поле тяжести Земли является неравномерным движением
и совершается по закону х = Vср(1, 0) = в то время как для второй секунды движения (t1 = 2, t0 = 1) она уже равна в три раза большему значению: Vср(2, 1) = Средняя скорость не может полностью характеризовать неравномерное движение. Для полной характеристики вводят так называемую мгновенную скорость. Очевидно, что средняя скорость Vср (t1, t0) тем полнее характеризует движение за промежуток времени от t0 до t1, чем меньше длительность этого промежутка. Предел средней скорости за промежуток времени от t0 до t1 при t1, стремящимся к t0, называется мгновенной скоростью V(t0) в момент времени t0, т.е.:
б) Производная функции Определение. Пусть задана функция f(x), x Є(a; b), и пусть х0 – некоторая точка интервала (a; b). Предел f ′ (x0) = Функция, имеющая производную в некоторой точке, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием и обозначается с помощью штриха. в) Физический и геометрический смысл производной Если функция у = f(x) дифференцируема в точке х0, то ее график имеет
касательную в точке М0(х0; f(x0)), угловой коэффициент которой равен
г) Вычисление производной на основе ее определения. Исходя из определения производной, сформулируем следующее правило нахождения производной функции в точке: Чтобы вычислить производную функции f(x) в точке x0 нужно: 1) Найти f(x) - f(x0); 2) составить разностное
отношение 3) вычислить предел
разностного отношения при
д) Непрерывность дифференцируемой функции. Сформулируем и докажем необходимое условие существования производной. Теорема: Если функция f(x) имеет производную в точке x0, то она непрерывна в этой точке. Согласно условию теоремы функция f(x) в точке x0 дифференцируема, т.е. существует предел:
Используя свойство предела, запишем это равенство в следующем виде:
где
где
Последнее означает непрерывность функции f(x) в точке x0. Замечание. Из доказанной теоремы легко усмотреть, что если функция не является непрерывной в некоторой точке, то она в этой точке не имеет производной. Таким образом, непрерывность в точке – необходимое условие дифференцируемости в точке. Далее заметим, что непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, т.е. из непрерывности функции в точке не следует ее дифференцируемость в этой точке. 3. Ответы на вопросы учащихся время 10 мин. 4. Закрепление нового материала время 20 мин. Самостоятельная работа по 4 вариантам САМОСТОЯТЕЛЬНАЯ РАБОТА ПО 4 ВАРИАНТАМ 1. Найти мгновенную скорость в момент времени t0 свободного падения тела в поле тяжести Земли (I, II, III, IV). 2. Точка движется
прямолинейно по закону x(t) = V0t + I в.: при t = 0 II в.: в момент t0 III в.: при t = 7 IVв.: в момент времени t = 7c 3. Найдите производную функции: I в.: f(x) = x2 II в.: f(x) = 2x3 + 4x + 4 III в.: f(x) = IVв.: f(x) = 3x2 + 4 4. Найдите производную функций в точках x = 1, x = 3. I в.: f(x) = II в.: f(x) = (x + 5)2 III в.: f(x) = 4 – x3 IVв.: f(x) = 5x4 + 2x3 – 3x + 6 5. Найдите производную функций в данных точках. I в.: f(x) = cos x, при х= II в.: f(x) = tg x, при х = III в.: f(x) =cos 2x, при х = IVв.: f(x) = x2 + 4x + 72, при х = -5 Подхожу к заключительной части урока, в которой подвожу итоги урока. Выделяю основные моменты темы, подчеркиваю необходимость изучения данной темы. Выдаю домашнее задание. Подвожу итоги урока. Выставляю оценки активным учащимся, для поощрения их потребности самообразования. III. Заключительная часть: время 3 мин. 1. Подведение итогов Еще раз выделяю наиболее важную информацию по производной. Определение. Пусть задана функция f(x), x Є(a; b), и пусть х0 – некоторая точка интервала (a; b). Предел f ′ (x0) = Функция, имеющая производную в некоторой точке, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием и обозначается с помощью штриха. Чтобы вычислить производную функции f(x) в точке x0 нужно: 1) Найти f(x) - f(x0); 2) составить разностное
отношение 3) вычислить предел
разностного отношения при
Теорема: Если функция f(x) имеет производную в точке x0, то она непрерывна в этой точке. Согласно условию теоремы функция f(x) в точке x0 дифференцируема, т.е. существует предел:
Используя свойство предела, запишем это равенство в следующем виде:
где
где
Последнее формула означает непрерывность функции f(x) в точке x0. Замечание. Из доказанной теоремы легко усмотреть, что если функция не является непрерывной в некоторой точке, то она в этой точке не имеет производной. Таким образом, непрерывность в точке – необходимое условие дифференцируемости в точке. Далее заметим, что непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, т.е. из непрерывности функции в точке не следует ее дифференцируемость в этой точке. 2. Задание на дом: повторение темы, № 229, 235, 238 3. Заключительное слово преподавателя: Прощаюсь с учениками.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
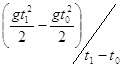 =
= 
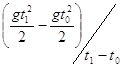 =
=