Курсовая работа: Моделирование физических процессов

ГОУ ВПО “Сибирский государственный университет телекоммуникаций и информатики”

Уральский технический институт связи и информатики (филиал)

Кафедра информационных систем и технологий

Моделирование физических процессов

Екатеринбург 2009

Оглавление

Введение

1. Математическая модель

2. Описание теории применяемой к задаче

3. Блок – схемы

4. Листинг программы

5. Фотография графика

6. Решение задачи в MathCAD

Вывод

Литература

Введение

Благодаря данной курсовой работе, я получу основные навыки: в моделирование физических процессов, грамотного распределения информации и грамотного использования возможностей языка программирования Pascal.

Курсовая работа является первой объёмной самостоятельной работой для меня в роли программиста. Эта работа завершает подготовку по дисциплине “Программирование на языках высокого уровня” и становится базой для выполнения последующих курсовых проектов по специальным дисциплинам. После выполнения данной курсовой работы, я рассчитываю научиться строить графики функций, работать в MathCAD, и понимать геометрический смысл методов: Эйлера модифицированного и Рунге-Кутта.

Математическая модель, постановка задачи.

1. Обсчитать первую точку методами Рунге–Кутта и Эйлера модифицированного.

2. Построить график к первой точке.

3. Составить блок - схемы.

4. Написать программу.

5. Построить график в MathCAD.

6. Сделать выводы

1. Математическая модель

Метод Рунге-Кутта

Теория:

Пусть дано дифференциальное уравнение первого порядка

= f(x, y), с начальным условием y() = .

Выберем шаг h и введём обозначения:

= + i*h , = y(), где

i = 0, 1, 2, …

- узлы сетки,

– значение интегральной функции в узлах.

Аналогично Модифицированного метода Эйлера решаем дифференциальное уравнение. Отличие состоит в делении шага на 4 части.

Согласно методу Рунге – Кутта 4 порядка, последовательные значения искомой функции y определяются по формуле:

= + ∆y, где

∆ = (+ 2 + 2 + ), I = 0, 1, 2, …

А числа , , , на каждом шаге вычисляются по формулам:

h* f(, )

, )

h* f(, + )

Обсчёт первой точки методом Рунге-Кутта:

Задано уравнение движения материальной точки: = x*sin(t), с условием

t 0 =1, t к =1.4, h = 0.05, x 0 =2.

Необходимо построить физическую и математическую модель движения.

tg(a) = x*sin(t) = 2*sin(1)= 1.6829

/(a) = 1.0346

t(b) = 1.6829 + 0.125 = 1.8079

x(b) = 2+0.125*1.8079 = 2.2259

tg(b) = 2.2259*sin(1) = 1.8730

/(b) = 1.0803

t(c) = 1.6829 + 0.025 = 1.7079

x(c) = 2 + 0.025*(1.7079) = 2.0426

tg(c) = 2.0426*sin(1) = 1.7187

/(c) = 1.0438

t(d) = 1.6829 + 0.0375 = 1.7204

x(d) = 2 + 0.0375*1.7204 = 2.0645

tg(d) = 2.0645*sin(1) = 1.7372

/(d) = 1.0484

Обсчет первой точки модифицированным методом Эйлера

Заданно уравнение движения материальной точки: = x*sin(t), с условием

t 0 =1, t к =1.4, h = 0.05, x 0 =2.

Необходимо построить физическую и математическую модель движения.

A(1 ; 2)

tg(a) = x*sin(t) = 2*sin(1)= 1.682

/(a) = 1.034

= + * f(, )

= 2 + 0.025*(1.6829) = 2.042

C(0.025 ; 2.042)

tg(c) = x*sin(t) = 2*sin(1.025) = 1.709

/(c) = 1.041

= +h*f(+ ; +*f(;))

= 2 + 0.05*(1.041) = 2.05205

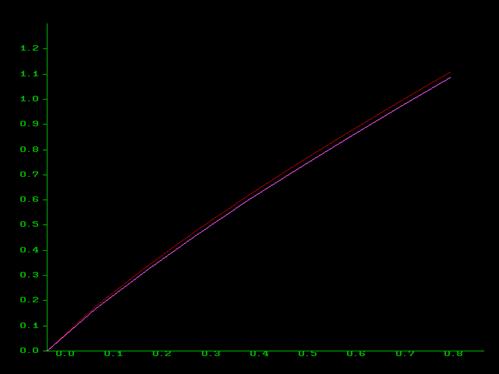
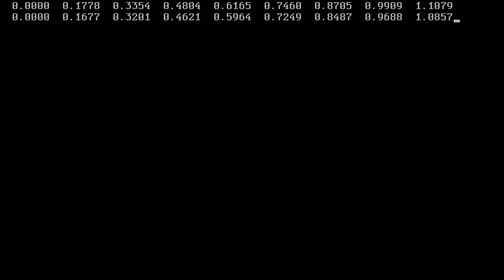
Таблица измерений в Pascal, Mathcad:

t	X1	X2	Xm
0	0	0	0
0.1	0.1778	0.1677	0.168
0.2	0.3354	0.3201	0.32
0.3	0.4804	0.4621	0.462
0.4	0.6165	0.5964	0.596
0.5	0.7460	0.7249	0.725
0.6	0.8705	0.8487	0.849
0.7	0.9909	0.9688	0.969
0.8	1.1079	1.0857	1.086

X1 – метод Эйлера модифицированный, X2 – метод Рунге – Кутта, Xm – решение в Mathcad

Фотография графика.

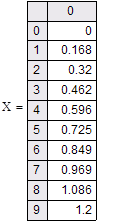
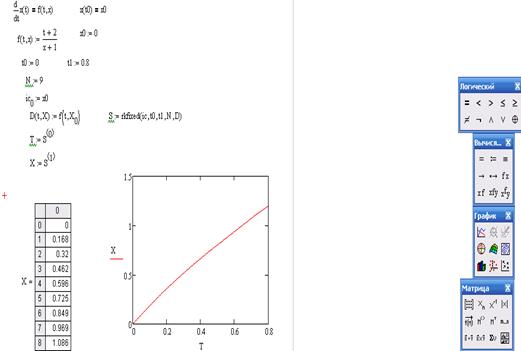
Решение в Mathcad

Вывод

В результате проделанной работы, я научился решать дифференциальные уравнения и строить к ним график, еще я научился решать такие уравнения в среде Turbo Pascal. Узнал, как решать различные уравнения в MathCAD. Еще я понял, как можно строить различный функции по точкам, с помощью циклов. Так же я понял, как нужно правильно масштабировать графики, в зависимости от заданной функции. Вследствие того, что данная курсовая, была для меня первой серьезной и объемной работой, я научился оформлять серьезные работы.

Список литературы

1. Демидович Б.П., Марон И.А., Шувалова Э.З., Численные методы анализа: Физматгиз, 1963.

2. Немюгин С.А. turbo Pascal. Практикум – СПБ.: Питер, 2005.

3. Немюгин С.А. turbo Pascal. Программирование на языке высокого уровня: Учебник для вузов. – СПБ.: Питер, 2009.

4. М.М. Боженова, Л.А. Москвина. Практическое программирование. Приемы создания программ на языке Паскаль.

5. Основные процедуры и функции модуля graph: http://rsc-team.ru/cgi-bin/index.pl?rzd=2&group=lection&ind=21