- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Лабораторная работа: Графы. Основные понятияЛабораторная работа: Графы. Основные понятияМинистерство образования и науки Российской Федерации Курский государственный технический университет Кафедра ПО ВТ и АС Лабораторная работа № 1 Графы. Основные понятия Выполнил: студент гр. ПО 62 Шиляков И.А. Проверил: доцентТомакова Р.А. Курск 2007 Задание: 1. По заданным матрицам смежности вершин восстановить графы. 2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости. 3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов. 4.
Найти композицию
графов 5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф. 6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл. 7. Определить хроматические и цикломатические числа данных графов. 8. Найти все базы графа. 9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа. Выполнение:
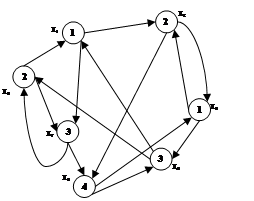
1. По заданным матрицам смежности вершин восстановить графы.
A1

G1(X1,A1)
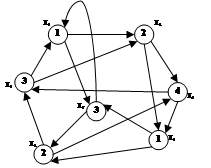
A2

G2(X2,A2) 2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
B1
B2
S1
S2
R1 R2
Q1 Q2 3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов. Объединение графов
G3(X3,A3)=G1(X1,A1) YG2(X2,A2); X3= X1YX2, A3= A1YA2 Пересечение графов
G3(X3,A3)=G1(X1,A1) ∩G2(X2,A2); X3= X1∩X2, A3= A1∩A2
Кольцевая сумма графов
G3(X3,A3)=G1(X1,A1) 4.
Найти и построить композицию
графов
G2(G1(Х)) 5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф. Остовные подграфы
G’1(X1,A1)
G’2(X2,A2) Произвольные подграфы
G1’’ (X1’’,A1’’)
Порожденные подграфы
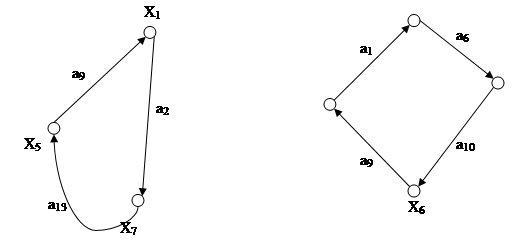
G1P(X1P,A1P) G2P(X2P,A2P) 6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл. Локальные степени графа G1
Локальные степени графа G2
Эйлерова цепь существует в двух графах, т.к. все локальные степени графов четны. Эйлеров цикл существует в двух графах, т.к. все локальные степени графов четны. 7. Определить хроматические и цикломатические числа данных графов.
Хроматическое число γ для графа G1 = 4
Хроматическое число γ для графа G2 = 4 Цикломатические числа графов V(G1)=m-n+r, где m - число рёбер (дуг); n – число вершин; r – число компонент связности. V(G1)=14-7+1=8; V(G2)=14-7+1=8; 8. Найти все базы графа. Базы графа G1 B1={x1} B2={x2} B3={x3} B4={x4} B5={x5} B6={x6} B7={x7} Базы графа G2 B1={x1} B2={x2} B3={x3} B4={x4} B5={x5} B6={x6} B7={x7} 9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа. Сильные компоненты связности G1 СК={x1, x2, x3, x4, x5, x6, x7} Сильные компоненты связности G2 СК={x1, x2, x3, x4, x5, x6, x7}
Конденсация графа G1 Конденсация графа G2 |



 G1(G2(Х))
G1(G2(Х))