- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Реферат: Дефокусировка. Сферическая аберрация 3 порядка. Кома и неизопланатизмРеферат: Дефокусировка. Сферическая аберрация 3 порядка. Кома и неизопланатизмБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра ЭТТ РЕФЕРАТ На тему: «Дефокусировка. Сферическая аберрация 3 порядка. Кома и неизопланатизм» МИНСК, 2008 Дефокусировка
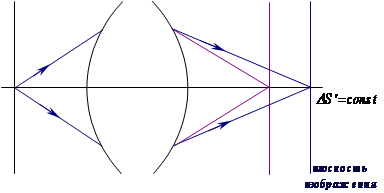
Дефокусировка не приводит к нарушению гомоцентричности пучка (рисунок 1), а только свидетельствует о продольном смещении плоскости изображения.
Рисунок 1 – Дефокусировка При дефокусировке все лучи на выходе оптической системы пересекаются в одной точке, но не в точке идеального изображения. Поэтому в случае дефокусировки продольная аберрация постоянна для всех лучей (для всех точек зрачка):
Если дефокусировки нет, то плоскость изображения совпадает с плоскостью Гаусса (плоскостью идеального изображения). Чтобы избавиться от дефокусировки, нужно просто соответствующим образом передвинуть плоскость изображения. При анализе аберраций оптических систем принято строить графики зависимости поперечной, продольной, и волновой аберраций от зрачковых координат. Если в оптической системе присутствует только дефокусировка, то эти графики будут выглядеть как показано на рисунке 2.
Рисунок 2 – Графики аберраций для расфокусировки Сферическая аберрация 3 порядка
Сферическая аберрация приводит к тому, что лучи, выходящие из осевой точки предмета, не пересекаются в одной точке, образуя на плоскости идеального изображения кружок рассеяния (рис.3). Ею обладают все линзы со сферическими поверхностями. Чтобы ее устранить, необходимо сделать поверхности не сферическими. Сферическую аберрацию 3 порядка называют также первичной сферической аберрацией.
Рисунок – 3. Сферическая аберрация Продольная и поперечная аберрации в этом случае определяются выражениями:
В простых положительных линзах сферическая аберрация 3 порядка отрицательна, а в отрицательных положительна. Графики волновой, продольной и поперечной аберраций в случае сферической аберрации 3 порядка представлены на рис.4.
Рисунок 4 - Графики аберраций для сферической аберрации 3 порядка Сферическая аберрация 5 порядка
По характеру искажения гомоцентричности пучка лучей сферическая аберрация 5 порядка полностью аналогична сферической аберрации 3 порядка, только имеет более высокий порядок кривых на графиках поперечной и продольной аберраций. В сложных системах
сферические аберрации 3 и 5 порядков имеют разные знаки и могут взаимно
компенсировать друг друга. На рис.5 представлен график оптимальной коррекции
сферической аберрации 3 и 5 порядков для апертурного луча
Рисунок 5 - Взаимокомпенсация сферической аберрации 3 и 5 порядков Однако в случае сферической аберрации 3 и 5 порядков может быть и так, как показано на рис.6.: а) – аберрация «недоисправлена», б) – аберрация «переисправлена».
Рисунок 6 - Графики коррекции сферической аберрации. Поскольку продольной дефокусировкой легко управлять путем перемещения плоскости изображения, то сочетая сферическую аберрацию и дефокусировку, можно выбрать наилучшее с точки зрения минимума главный луч сферической аберрации положение изображения. В частности, для сферической аберрации 3 порядка при помощи выражений (4), (5) можно вычислить положение изображения, в котором кружок рассеяния минимален. При этом продольное смещение изображения составляет 3/4 от продольной аберрации апертурного луча. Кома От греческого: kωμα – хвост, пучок волос. Кома появляется при смещениях точки предмета с оси. Кома добавляется к другим аберрациям (например, к сферической), но мы будем рассматривать ее отдельно от других аберраций (рис.7).
Рисунок 7 - Структура пучка лучей при наличии комы. В первом приближении кома прямо пропорциональна смещению предмета с оси. Если смещение равно нулю, то и кома равна нулю. Таким образом, поперечная аберрация при наличии комы прямо пропорциональна величине предмета:
где d – коэффициент пропорциональности, определяющий качество аберрационной коррекции оптической системы (чем меньше d, тем лучше оптическая система). Разложение в ряд волновой аберрации при наличии комы 3 и 5 порядков:
или Выражение для поперечных аберраций будет выглядеть следующим образом:
Описание поперечных
аберраций комы различно для меридионального и сагиттального сечений. В
меридиональном сечении
В сагиттальном сечении
На рис.8 показаны графики
поперечных аберраций для комы 3 порядка в меридиональном и сагиттальном сечениях.
Кривые на графиках имеют одинаковую форму, но в меридиональном сечении значение
Рисунок 8 - Поперечные аберрации при коме 3 порядка Для того чтобы лучше понять структуру поперечных аберраций при коме, рассмотрим точечную диаграмму лучей. Разобьем зрачок на множество равновеликих площадок и рассмотрим лучи, проходящие через центры этих площадок (рис.9.а). Получим картину лучей, равномерно распределенных по зрачку. Точки пересечения этих лучей с плоскостью изображения образуют точечную диаграмму (рис.9.б).
Рисунок 9 - Точечная диаграмма Кома и неизопланатизм В названии “неизопланатизм” присутствуют корни греческих слов: изос – одинаковый, равный, планета – блуждающее тело. Изопланатизм (одинаково заблуждающийся) – в окрестности оси оптической системы нет комы, но есть сферическая аберрация (изображение разных точек предмета будет одинаково плохое). Апланатизм – нет ни комы, ни сферической аберрации (изображение разных точек предмета идеальное). Апланатизм может выполняться только для какой-то части предмета, например в окрестности оси. О возможной величине комы можно судить, не смещая точку с оси, если количественно оценить неизопланатизм. Такая оценка возможна, если использовать условия апланатизма и изопланатизма. Закон синусов Аббе (условие апланатизма):
Если это условие выполняется для всех лучей, то нет ни комы, ни сферической аберрации. Если присутствует сферическая аберрация, то вместо условия апланатизма используется похожее условие – условие изопланатизма:
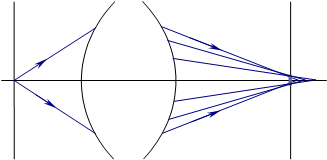
Рис. 10 показывает разницу в определении двух условий – условия синусов Аббе и условия изопланатизма.
Рисунок 10 - Углы лучей, используемые в условиях апланатизма и изопланатизма. Если условие изопланатизма выполняется, то комы в ближайшей окрестности осевой точки не будет. Относительное отступление от изопланатизма (так называемая мера комы) определяется следующим выражением:
Поперечная аберрация комы
3 порядка для точки изображения с координатой
ЛИТЕРАТУРА 1. Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. – М.: Машиностроение, 2004 2. Заказнов Н.П. Прикладная оптика. – М.: Машиностроение, 2000 3. Дубовик А.С. Прикладная оптика. – М.: Недра, 2002 4. Нагибина И.М. и др. Прикладная физическая оптика. Учебное пособие.- М.: Высшая школа, 2002 |





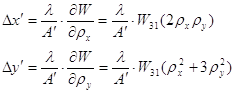 . (8)
. (8) 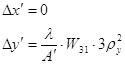 (9)
(9) 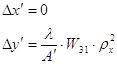 .
(10)
.
(10) 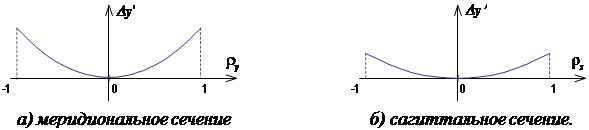

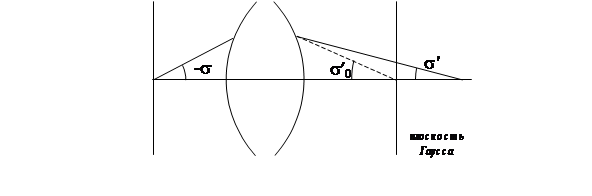
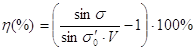 .
(13)
.
(13)