- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
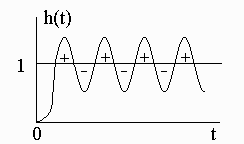
Реферат: Интегральные методы оценки качества переходных процессовРеферат: Интегральные методы оценки качества переходных процессовРеферат на тему: "Интегральные методы оценки качества переходных процессов" Введение Интегральная оценка является обобщенным показателем качества переходного процесса, при этом качество системы оценивается с помощью числа, являющегося интегралом некоторой функции. Особенность интегральной оценки в том, что в отличии от других методов оценки качества, величина интеграла представляет число, которое ничего не говорит о характере переходного процесса, о конкретных показателях качества, зато, в сравнении с другими, метод отличается простотой. Линейная интегральная оценка Рассмотрим переходные процессы, приведенные на рис. 1а-в.
а б вРис. 1Заштрихованная площадь называется площадью регулирования, она может быть оценкой качества переходного процесса. Чем меньше площадь, тем лучше качество переходного процесса. Площадь регулирования может быть определена с помощью интеграла, который называется простой (линейной) интегральной оценкой
|
|||||||||||||||||||||||||||||||
|
||||
 |
||||
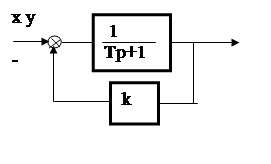
Рис. 3
3. Определим величину интеграла J1
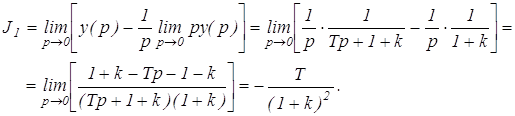
Интегральная квадратичная оценка
Интегральная квадратичная оценка пригодна для любых переходных процессов, и вычисляется по формуле
![]() (6)
(6)
Подинтегральное выражение – z2(t) всегда положительно не зависимо от знака функции z(t).
Определим J2 без расчета переходного процесса, для этого воспользуемся дуальной теоремой.
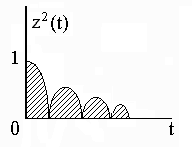
Рис. 4
Основная теорема: произведению изображений соответствует свертка оригиналов
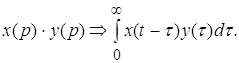 (7)
(7)
Дуальная теорема: произведению оригиналов соответствует свертка изображений
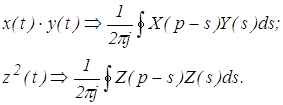 (8)
(8)
Так как 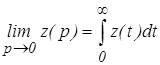 ,
,
то можно получить следующую формулу для расчета квадратичной интегральной оценки
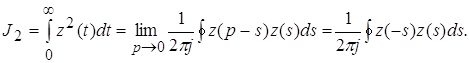 (9)
(9)
Этот интеграл можно вычислить либо с помощью вычетов по полюсам подинтегральной функции, либо с использованием табулированных значений интеграла для функции
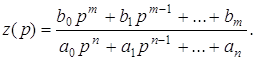 (10)
(10)
В таблице 1 приведены табулированные значения интеграла для n = 1 ¸ 3 для систем более высокого порядка таблицы приведены в литературе [5].
Таблица 1
| n |
J2 |
| 1 |
|
| 2 |
|
| 3 |
|
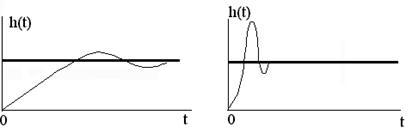
Недостаток метода. Рассмотрим переходные процессы (рис. 5).
а) б)
Рис. 5
При использовании этого метода два процесса могут иметь одинаковую площадь регулирования, но оба они плохие по различным показателям качества, у первого большое время регулирования, а во втором большое перерегулирование.
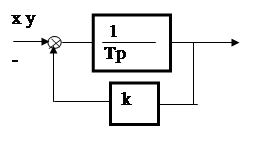
Пример 6. Вычислить величину J2 для заданной системы (рис. 6).
 |
|||
|
|||
Рис. 6
3. Определим z(p)
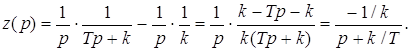
4. Определим величину интеграла J2 с помощью вычетов s1 = – k/T
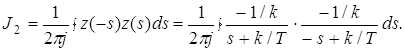
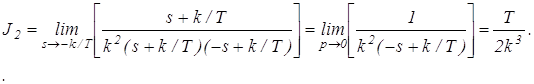
5. Определим величину интеграла J2 с помощью таблиц
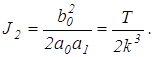
Модифицированная интегральная оценка
При использовании модифицированной (улучшенной) интегральной оценки минимизируем не только квадратичное отклонение z(t), но и его производную – z’ (t). Такой оценкой является интеграл
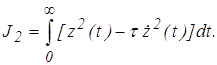 (11)
(11)
где t – постоянная времени.
Минимуму интеграла соответствует приближение переходного процесса не к ступенчатому, а к некоторому экспоненциальному с заданной постоянной времени (которая называется экстремалью). Применение этой оценки приводит к более пологим переходным процессам, т.е. менее колебательным и имеющим меньшее число перерегулирований.
Недостаток метода: Сложность выбора экстремали, она выбирается на основе опыта.
Достоинства и недостатки интегральных методов
Достоинства методов:
1. Простота.
2. Оценка качества является обобщенной (в виде одного числа), что удобно при оптимизации систем и для сравнительного анализа систем
Недостатки методов:
1. Каждый методов имеет свои специфические, ранее рассмотренные недостатки.
2. Величина интеграла представляет число, которое ничего не говорит о характере переходного процесса, т.е. о конкретных показателях качества.
Литература
1. Бесекерский В.А., Попов Е.П. «Теория систем автоматического управления». Профессия, 2003 г. – 752 с.
2. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
3. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В.А. Бесекерского. – M.: Наука, 1978.
4. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.
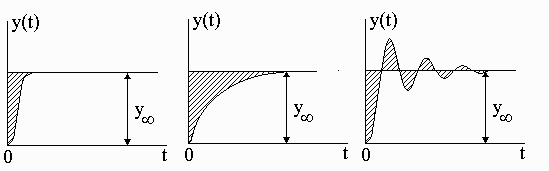
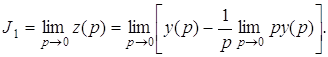 (4)
(4)