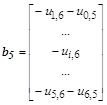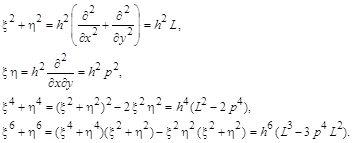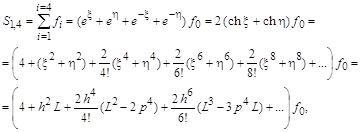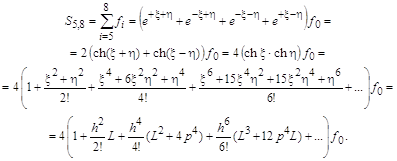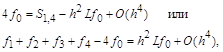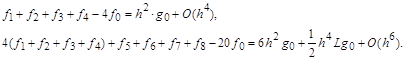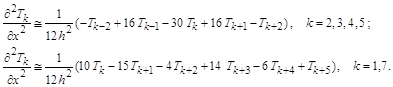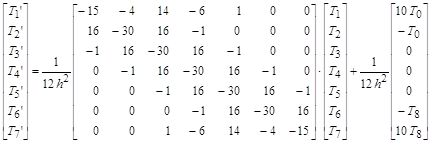- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Реферат: Краевые задачи и разностные схемыРеферат: Краевые задачи и разностные схемыРеферат з курсу “Введение в численные методы” Тема: “КРАЕВЫЕ ЗАДАЧИ И РАЗНОСТНЫЕ СХЕМЫ” Содержание 1. Приведение к системе уравнений первого порядка 2. Разностное представление систем дифференциальных уравнений 3. Разностные системы уравнений для краевых задач 4. Краевые задачи второго порядка 5. Разностные схемы для уравнений в частных производных 6. Повышение точности разностных схем 7. Сеточные методы для нестационарных задач Литература 1. Приведение к системе уравнений первого порядка Для решения систем дифференциальных уравнений высокого порядка методами конечных разностей в первую очередь возникает потребность преобразования исходной системы в систему дифференциальных уравнений первого порядка с соответствующим образом преобразованными начальными или граничными условиями. И уже далее реализовывать численную процедуру решения. Преобразование в систему уравнений первого порядка не единственно. Наиболее популярные из них в большинстве своем касаются линейных систем с постоянными или переменными коэффициентами. Основная идея всех методов состоит во введении новых переменных и выполнении замены высших производных этими переменными. Пусть неоднородное дифференциальное уравнение высокого порядка задано в виде:
где
Обозначим первую производную искомой
функции новой переменной
При таких заменах производных искомой
функции
В результате, эквивалентная система дифференциальных уравнений первого порядка примет следующий вид:
В случае, когда правая часть
представлена взвешенной суммой функции
то его преобразование в систему
уравнений первого порядка с новыми переменными
Такое преобразование сохраняет
коэффициенты исходного уравнения неизменными и исключает производные в правой
части от И, наконец, приведем еще один вариант разложения на систему уравнений первого порядка исходного неоднородного уравнения с производными в правой части:
Замена переменных в отличие от предыдущего случая производится без сохранения коэффициентов исходного уравнения:
Производные искомой функции
Умножив каждое выражение для Система уравнений имеет вид:
В векторно-матричной форме это уравнение и его решение записываются в следующем виде:
где
Обратная матрица удобна при
использовании математических пакетов для решения векторно-матричного уравнения.
Если Начальные условия для
или в векторно-матричной форме:
2. Разностное представление систем дифференциальных уравнений Представление системы дифференциальных уравнений первого порядка с начальными условиями
можно заменить системой
конечно-разностных уравнений первого порядка с целочисленной независимой
переменной i (
погрешность аппроксимации которого пропорциональна сеточному шагу h. Выше было уже показано, как можно
уменьшить погрешность аппроксимации, делая ее пропорциональной
При такой замене производной мы
получаем систему разностных уравнений, состоящую из разностных уравнений
второго порядка, требующих, кроме известного вектора начальных условий
Дополнительный вектор начальных условий достаточно вычислить по формуле Эйлера. Он и определит дополнительное начальное условие с ошибкой, пропорциональной второй степени h:
Подстановка таких начальных условий в
решение сохранит погрешность результатов на уровне 3. Разностные системы уравнений для краевых задач Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности - на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей. Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной. Для линейной системы уравнений
первого порядка, записанной в матричной форме относительно вектора
обязательно задается полный набор
краевых условий Обычно задаваемое граничное значение совмещается
с тем или иным n-ным сеточным значением независимой переменной. Это
позволяет обходиться без преобразования граничных условий к ближайшей точке
сетки. Векторы
Многоточечные представления производных получаются путем применения существующих соотношений между операторами дифференцирования, конечных разностей и сдвига:
Чтобы выразить значение производной
порядка k в m-той точке целочисленного интервала [0, n]
через ординаты функции
Заменив конечно-разностные операторы
Погрешность аппроксимации
дифференциального оператора конечно-разностным оператором для центральной точки
(m=n/2) пропорциональна с наименьшим коэффициентом величине Часто применяемые выражения конечно-разностной аппроксимации производных первого и второго порядков по трем-семи равномерно расположенным точкам приведены ниже в таблицах в виде коэффициентов, стоящих перед соответствующими ординатами функции. В левом верхнем углу таблиц записан общий множитель, а в крайней правой колонке – коэффициенты k1, k2 для формул погрешности. Трех точечная аппроксимация первой производной
Четырех точечная аппроксимация первой производной
Пятиточечная аппроксимация первой производной
Шести точечная аппроксимация первой производной
Семи точечная аппроксимация первой производной
Трех точечная аппроксимация второй производной
Четырех точечная аппроксимация второй производной
Пятиточечная аппроксимация второй производной
Шести точечная аппроксимация второй производной
Семи точечная аппроксимация второй производной
Например, производная первого порядка
Аналогично выписываются выражения и для вторых производных в точках 0 и 2:
Таким образом, из приведенных таблиц можно выбрать аппроксимирующие выражения для производной в данной точке, включающие значения функции в точках нужного окружения. 4. Краевые задачи для уравнений второго порядка При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями. Преобразование их в конечно-разностную систему алгебраических уравнений осуществляется аналогично: для каждой точки в области (интервале) интегрирования, где не задано краевое или граничное значение искомой функции, записывается исходное уравнение, в котором все производные выражены через заранее определенное число близлежащих ординат искомой функции, принадлежащих области, и вычислены все коэффициенты и функции независимых переменных в этой точке. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области. В результате будет сформирована алгебраическая система уравнений с числом уравнений и неизвестных, равном общему числу точек области интегрирования. В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Это достигается многократным применением оператора сдвига к соответствующему конечно-разностному оператору. Если в центральных точках точность аппроксимации производных с n точками удовлетворяет поставленным требованиям и эту точность желательно сохранить и в приграничных точках заданных областей, то для последних выбирают аппроксимирующие формулы, построенные для (n+1)-й точки или более. Рассмотрим примеры аппроксимации дифференциальных уравнений с краевыми условиями конечно-разностной системой алгебраических уравнений. Эти аппроксимации в литературе получили название "разностные схемы". Ниже в четырех таблицах приведены четыре варианта конечно-разностной аппроксимации одной и той же краевой задачи, для которой известно точное решение. Вид уравнения, условия на границе интервала, решение аналитическое и вычисленное в заданных точках с 12 значащими цифрами приведены в правой крайней колонке первой таблицы. В левых колонках первой и в трех остальных таблицах записаны системы алгебраических уравнений, полученных применением трех-, пяти-, пяти-шести- и семи точечной аппроксимации второй производной в заданном уравнении. Справа от уравнений приведены решения алгебраических уравнений тоже с 12-ю значащими цифрами.
В этой задаче весь интервал интегрирования [0,1] был разбит на 10 равных частей с шагом h=0.1. Из одиннадцати точек в двух крайних искомая функция x(t) была задана, поэтому уравнения записывались для девяти внутренних точек, в которых значения функции требовалось найти. 5. Разностные схемы для уравнений в частных производных Конечно-разностная аппроксимация дифференциальных уравнений в частных производных, называемая в литературе методом сеток, использует те же конечно-разностные выражения производных через значения искомой функции, которые приведены в таблицах выше. Однако есть особенности, которые связаны с наличием у каждой рассматриваемой точки соседних точек не только по направлениям осей независимых переменных, но и во множестве других наклонных направлений. Поэтому, в случае использования многоточечных (более трех точек) формул для производных, выражения последних могут разрабатываться дополнительно для каждого применения. Наиболее удобным в разработке многоточечных конечно-разностных выражений для уравнений в частных производных является операторный метод, основанный на учете взаимосвязи оператора дифференцирования с операторами сдвига по направлениям различных независимых переменных. Рассмотрим его применение на примере построения разностных формул для двумерных уравнений в частных производных второго порядка. Характерным представителем уравнений в частных производных второго порядка является уравнение Лапласа:
где Область численного решения уравнения разобьем на клетки системой вертикальных и горизонтальных прямых, проходящих через равномерно расположенные с шагом h точки на осях координат соответственно x и y:
Значения функции в узлах сетки
обозначим через
После подстановки в уравнение Лапласа этих выражений для каждой внутренней точки области будет получена система алгебраических уравнений следующего вида:
В качестве примера, демонстрирующего
применение метода сеток, приведем решение уравнения Лапласа для прямоугольной
области с количеством узлов
Уравнения для 25 внутренних точек u(i,k):
Результат решения системы из 25 уравнений представлен в таблице:
Следует отметить, что в трех точечном
представлении конечно-разностные выражения производных второго порядка для
внутренних и приграничных точек совпадают. Это позволяет для прямоугольных
областей, заменив двумерную индексацию неизвестных
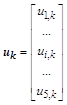
преобразовать систему уравнений в векторно-матричную форму записи с блочно-диагональной матрицей коэффициентов, которая удобна для решения алгебраических уравнений с числом неизвестных более 100 на векторных вычислительных машинах:
– матрицы, соответственно, блочная, коэффициентов и единичная;
– соответственно, векторы неизвестных и правых частей уравнения со своими блочными компонентами. В конечно-разностном представлении уравнения Лапласа каждое уравнение является для соответствующей точки области формулой вычисления среднего арифметического совокупности значений функции в соседних точках:
Погрешность конечно-разностного представления уравнения Лапласа в виде системы алгебраических уравнений определяется погрешностью аппроксимации производных, которая для трех точечного варианта, приведенного выше, пропорциональна шагу сетки. Естественно желание повысить точность аппроксимации лапласиана, добавив в структуру его конечно-разностного представления значения функции в дополнительных точках при сохранении суммирования значений из окружающих точек. 6. Повышение точности разностных схем Оператор сдвига, преобразующий
значение функции в точке z в значение функции в точке z+h выражается
через оператор производной
Обозначив операторные выражения для сдвига значений функции по осям x, y соответственно
несложно записать с их помощью следующие операторные выражения:
Во фрагменте сетки, изображенной в
виде таблицы
Вычислим суммы значений функций, симметрично располагающихся вокруг центральной точки:
Подобными преобразованиями операторных выражений можно получить формулы для следующих сумм:
Включая выражения для частичных сумм в единую сумму с различными весовыми коэффициентами, пренебрегая выражениями с производными и лапласианами высоких порядков, получают конечно-разностные формулы, аппроксимирующие уравнение Лапласа в заданной точке и содержащие большее число значений искомой функции. Например, из выражения для
что, после пренебрежения слагаемыми в
правой части, полностью соответствует трех точечной разностной аппроксимации
частных производных. Суммируя
Если значения частных производных в точках области решения малы, то радикальным способом увеличения точности аппроксимации уравнения является уменьшение шага сетки. При задании в правой части уравнения
Лапласа функции g(x,y) последняя в приведенных конечно-разностных
суммах должна заменить
7. Сеточные методы для нестационарных задач Уменьшение величины шага приводит к квадратичному возрастанию числа точек в области решения, а следовательно, к порядку алгебраической системы уравнений. Одним из путей уменьшения числа уравнений является метод прямых, который позволяет аппроксимировать дифференциальное уравнение в частных производных системой дифференциальных уравнений в обыкновенных производных с краевыми условиями. Для этого частные производные по одной из независимых переменных не заменяют конечно-разностным эквивалентом. Если в уравнении оставлена пространственная переменная, то получаемая система будет краевой задачей со всеми сложностями ее решения, рассмотренными ранее. Существенным будет выигрыш лишь при решении дифференциальных уравнений в частных производных, описывающих нестационарные процессы. К ним относятся уравнения, подобные уравнениям теплопроводности и волновому. Этим уравнениям кроме условий на границе задают еще и начальное распределение искомой функции во всех точках области решения. Применение метода прямых рассмотрим на примере решения уравнения теплопроводности следующего вида:
которое описывает распространение тепла (изменение температуры) вдоль металлического стержня, вваренного своими концами в две металлические пластины с разными, постоянно поддерживаемыми на них температурами. Коэффициент B, характеризующий свойства материала, возьмем равным 1. Пусть расстояние между пластинами
равно единице, т.е. Разобьем единичную длину стержня на 8
равных частей (h=1/8) и обозначим значение температуры в каждой
точке через
После замены производных
конечно-разностными эквивалентами получим следующую систему линейных
дифференциальных уравнений с начальными условиями
Чтобы получить представление о влиянии порядка разностных формул на вид записи и точность решения задачи, в таблице приведены системы уравнений для 5- и 3-точечных выражений частных производных:
Полученные системы обыкновенных
дифференциальных уравнений можно решать любым из рассмотренных ранее численным
методом. Правда, появляется особенность в выборе шага интегрирования по
времени, который теперь зависит еще и от шага разбиения области решения по
пространственной переменной. В случае аппроксимации производной по времени
конечными разностями “вперед” соотношение между шагом по временной переменной В рассматриваемом примере
Как видно, трех точечная аппроксимация по сравнению с пятиточечной дает худший результат. Точное решение в установившемся режиме дает изменение температуры на каждой одной восьмой длины стержня 12,5°С. Пятиточечная аппроксимация в данной задаче дала погрешность в сотые доли процента. Литература 1. Калашников В. И. Введение в численные методы: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 132 с. 2. Рено Н.Н. АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ: МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВУЗОВ. Изд-во: "Книжный дом Университет" (КДУ), 2007. – 24с. 3. Самарcкий А. А. Задачи и упражнения по численным методам. Изд.3 Изд-во: КомКнига, ЛКИ, 2006. – 208с. 4. Самарский А.А. Введение в численные методы Учебное пособие для вузов 3-е изд.,стер. ЛАНЬ, 2005. – 288с. 5. Турчак Л. И., Плотников П. В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304с. 6. Тыртышников Е.Е. МЕТОДЫ ЧИСЛЕННОГО АНАЛИЗА (1-Е ИЗД.) УЧЕБ. ПОСОБИЕ Издательство "Академия/Academia", 2007. – 320с. |
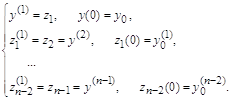
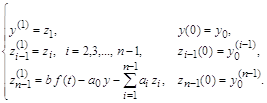
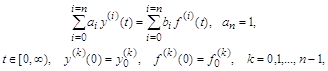
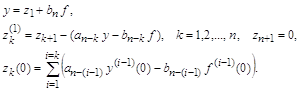
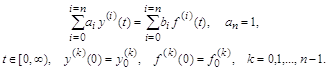
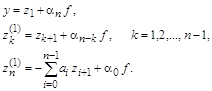
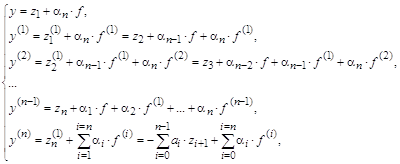
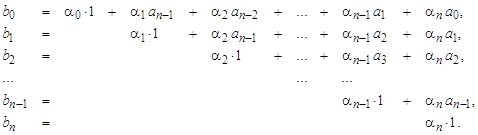
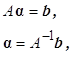
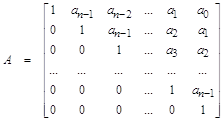 .
.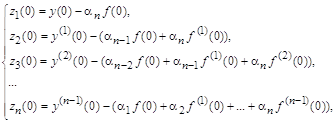
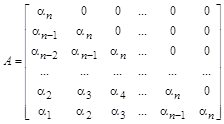 .
.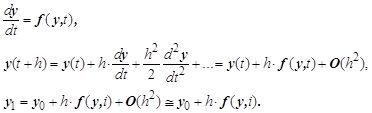
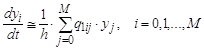 .
.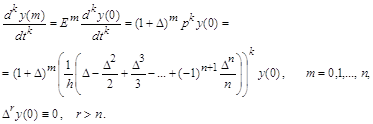
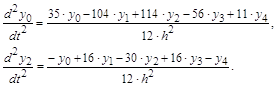
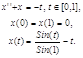
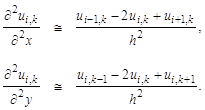
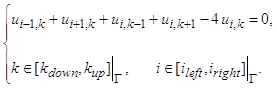
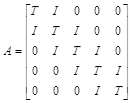 ,
, 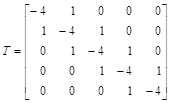 , I
, I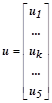 ,
,  ,
, 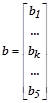 ,
,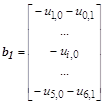 ,
, 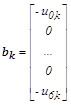 ,
,