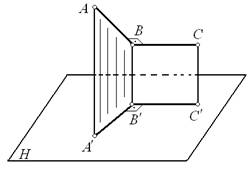
Реферат: Перпендикулярность геометрических элементов

План

1. Теорема о проецировании прямого угла

2. Главные линии плоскости

3. Прямая, перпендикулярная к плоскости

4. Перпендикулярные плоскости

5. Перпендикулярные прямые

1. Теорема о проецировании прямого угла

Возможны три случая проецирования прямого угла:

1. Если обе стороны прямого угла прямые общего положения, то прямой угол проецируется искаженно на все три плоскости проекций.

2. Если обе стороны прямого угла параллельны какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину.

3. Если одна сторона прямого угла параллельна какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину, рис. 64. Это основная теорема о проецировании прямого угла.

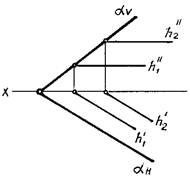
Рис. 64

Дано: Ð АВС = 90°; ВСúú Н. Необходимо доказать: ÐА¢В¢С¢ = 90°.

1. ВС ^ АВВ¢А¢

ВС ^ АВ, следовательно ВС ^ ВВ¢ - по свойству ортогонального проецирования

2. В¢С¢úú ВС

3. В¢С¢^ АВВ¢А¢

4. В¢С¢^ А¢В¢ - что и требовалось доказать

2. Главные линии плоскости

Линии уровня плоскости

Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.

Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 65). Горизонтальный след плоскости — одна из горизонталей.


Рис. 64	Рис. 65

Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 66).

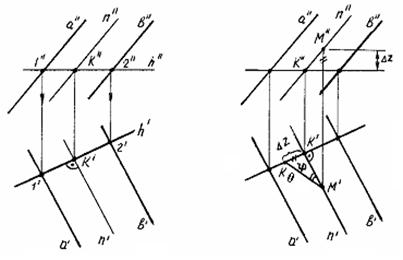
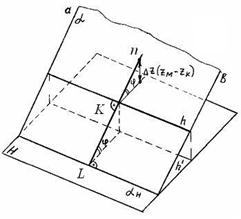
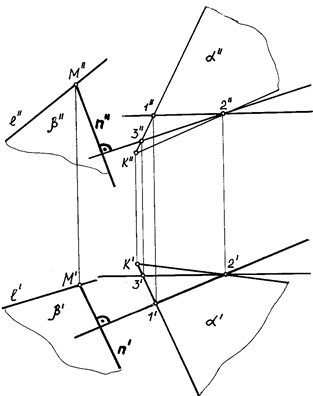
Рис. 66

Линии наибольшего наклона плоскости

Прямые плоскости, перпендикулярные к прямым уровня этой плоскости, называются линией наибольшего наклона (ЛНН) данной плоскости к соответствующей плоскости проекций.

Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 67).

В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.

На рис. 67, 68 дано изображение плоскости  (а || b), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.

Проведем в данной плоскости горизонталь h (рис. 68). Прямая n, перпендикулярная к прямой h, перпендикулярна и к следу плоскости H (KL^H) (рис. 69).

Рис. 67

Угол наклона прямой n к плоскости H определяется как угол между прямой и ее проекцией на плоскость H. Строим KK¢^H (рис. 69). Тогда угол j — искомый угол наклона прямой n к плоскости H.

На рис. 68 построена линия наибольшего наклона плоскости  к горизонтальной плоскости проекций — прямая n. Угол наклона плоскости  к плоскости H получают при определении натуральной величины отрезка KM при построении прямоугольного треугольника по проекциям K¢M' и .

Рис. 69

3 Прямая, перпендикулярная к плоскости

Прямая, перпендикулярная к плоскости, если перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. На основании теоремы о проецировании прямого угла в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.

Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.

Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция — фронтальной проекции фронтали (рис. 70) или соответствующим следам плоскости (рис. 71).


Рис. 70	Рис. 71

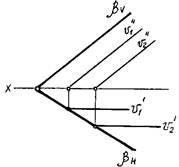
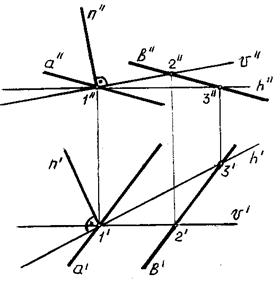
На рис. 72 изображена плоскость общего положения  (a|| b), к которой к которой требуется провести перпендикулярную прямую.

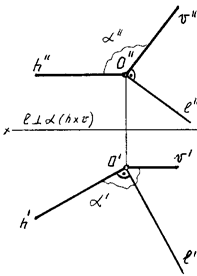
Рис. 72

Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 72).

Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:

n¢ ^ h¢; n² ^ h².

Построенная прямая n (n', n'') является искомым перпендикуляром к плоскости .

4. Перпендикулярные плоскости

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную данной плоскости. Построение таких плоскостей может быть выполнено двумя путями:

1) плоскость проводится через перпендикуляр к другой;

2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.

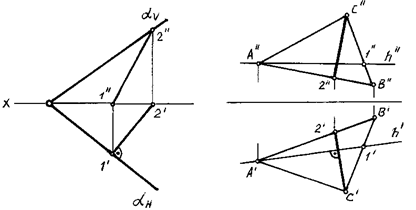
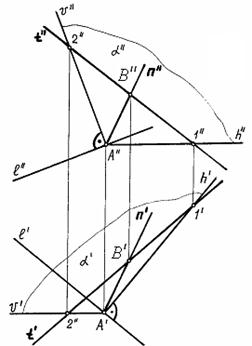
На рис. 73 изображены прямая общего положения и плоскость общего положения  (а ´ b). Требуется построить через прямую плоскость, перпендикулярную к плоскости .

Рис. 73

Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости , заданной пересекающимися прямыми a и b.

Проводим в плоскости  горизонталь h и фронталь v (рис. 73).

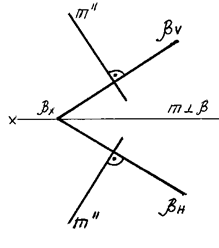
Далее из точки М, взятой на прямой , опускаем перпендикуляр n, пользуясь рассмотренным выше положением: n' ^ h'; n'' ^ v'', т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция — перпендикулярна фронтальной проекции фронтали (рис. 73).

Плоскость  (Ç n), проходящая через прямую n, будет перпендикулярна к плоскости .

6.5 Перпендикулярные прямые

Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.

На рис. 74 изображена прямая общего положения, к которой требуется провести перпендикулярную прямую.

Рис. 74

Через точку А прямой строим перпендикулярную к ней плоскость  (h Ç v) (рис. 71):

' ^ h'; '' ^ h''.

Любая прямая, лежащая в плоскости  будет также перпендикулярна к данной прямой . Поэтому проведем в этой плоскости произвольную прямую t, на которой возьмем произвольную точку, например, точку В (рис. 74).

Соединив точки А и В, лежащие в плоскости, получим прямую n, перпендикулярную к данной прямой (рис. 74).