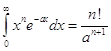- Главная
- Авиация и космонавтика
- Административное право
- Акционерное право
- Английский
- Антикризисный менеджмент
- Биографии
- Автомобильное хозяйство
- Автотранспорт
- Культура и искусство
- Маркетинг
- Международное публичное право
- Международное частное право
- Международные отношения
- Менеджмент
- Металлургия
- Муниципальное право
- Налогообложение
- Оккультизм и уфология
- Педагогика
- Политология
- Право
- Предпринимательство
- Психология
- Радиоэлектроника
- Риторика
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технологии
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право и процесс
- Управление
- Сочинения по литературе и русскому языку
- Другое
Учебное пособие: Введение в теорию атомаУчебное пособие: Введение в теорию атомаВведение в теорию атома. Краткие математические сведения о сферических системах. Ротатор. Уравнение Шрёдингера для одноэлектронного атома (атом водорода и водородоподобные ионы). 8.1. Краткое содержание. Шаровые координаты (r, J, j). Элемент объёма. Лапласиан в шаровых координатах. Уравнение Лапласа в сферических переменных. Роль симметрии в выборе радиальной части общего решения. Угловая часть уравнения Лапласа - уравнение Лежандра. Оператор момента импульса, его квадрат в шаровых переменных и его связь с уравнением Лежандра. Ротатор. Квантование модуля момента импульса ротатора. Операторные уравнения для момента импульса и их связь с уравнением Лежандра. Уравнение Шрёдингера для электрона в атоме водорода. Разделение переменных. Радиальная и угловая части уравнения Шрёдингера и вид общего решения. Квантование модуля и проекций момента импульса электронного вращения вокруг ядра. Квантование энергии и энергетические уровни. Пределы изменения квантовых чисел. Боровский радиус и его вероятностный смысл. Одноэлектронный гамильтониан в шаровых координатах и уравнение Шрёдингера для атома водорода (или водородоподобного иона). Разделение переменных. Атомные орбитали, их радиальные и угловые компоненты:
Квантовые числа (n,l,m), их взаимосвязь, пределы изменения и физический смысл. Квантование энергии, модуля и проекций момента импульса электрона на атомных орбиталях. Полярные диаграммы угловых компонент АО. Раздел в значительной степени предназначен для начинающего читателя и одна из его целей – упражнения в элементарной алгебре линейных операторов. 8.2. Предварительная общая информация. Сферические переменные. Уравнение Лапласа. Атом водорода. Уравнение Шрёдингера. Разделение переменных (иллюстрации и основные формулы) Радиальная переменная r, азимутальная переменная (угол широты) J, переменная широты (угол широты) j . Квантовые числа.
Радиальная переменная r Угол широты J Угол долготы Декартовы координаты:
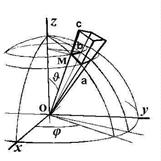
Интервалы изменения шаровых переменных: 0<r<¥; 0<J <; 0<j <2 Интервалы изменения переменных дают возможность выявить вид полярных диаграмм угловых функций - решений операторных уравнений. Элемент объёма в шаровых переменных (см. рис.):
8.3 Лапласиан. Важное свойство лапласиана состоит в его симметрия ко взаимным перестановкам декартовых координат. Из этого свойства вытекают и приёмы решения наиболее распространённых дифференциальных уравнений в частных производных с его участием.
Простейшее дифференциальное уравнение в частных производных второго порядка, в котором лапласиан играет основную роль - уравнение Лапласа. В шаровых координатах лапласиан оказывается составленным из трёх независимых компонент-операторов, каждый из которых преобразует лишь одну из трёх независимых пространственных переменных. Симметрией конкретной системы предопределяется выбор координат, в которых следует выразить лапласиан, ею определяется вид решений дифференциальных уравнений, в которых уравнение Лапласа оказывается в роли однородной части. Таковы две задачи о сферически симметричных движениях. Первая из них о свободном вращении без потенциальной энергии. Вторая о вращении в поле центральной силы. Основная квантово-механическая модель, применяемая для исследования сферического вращения как с потенциальной энергией, так и без неё, называется РОТАТОР. Первая задача о стационарном вращении частиц с линейно распределённой массой относительно центра масс. Таковы все двухатомные молекулы, а также некоторые трёхатомные молекулы, такие как CO2, CS2. Эта задача более проста, и в ней вращение частицы свободное, т.е. совершается без потенциальной энергии (Urot=0), и единственный вклад в энергетические уровни даёт лишь кинетическая энергия вращения. В классической механике энергию такого движения можно было бы отождествить с энергией чисто тангенциального (касательного) перемещения частицы по сфере. Вторая задача о стационарном движении с потенциальной энергией в поле центральной силы. В классическом рассмотрении наряду с тангенциальной, чисто вращательной, появилась бы и радиальная компонента энергии. В атомах существенную роль играет лишь электростатическое взаимодействие, подчиняющееся закону Кулона. Силы гравитации по сравнению с ним неизмеримо мала. Для одного электрона в поле ядра с порядковым номером Z в Периодической Системе Менделеева потенциальная энергия притяжения в системе СГС равна U(r) = - Z×e2/r. 8.4. Одноэлектронные атомы. Одноэлектронными сферически симметричными системами являются атом водорода, водородоподобные ионы (ионы, ядра которых имеют порядковые номера Z, в поле которых находится всего 1 электрон. Такие ионы образуются при Z-1 ступенчатой ионизации), а также атом позитрония, который образуется перед аннигиляцией электрон - позитронной пары в виде стационарной системы перед тем, как они аннигилируют, излучая два гамма-кванта. 8.5. Перевод лапласиана в шаровые координаты можно осуществить, следуя различным схемам. В сферических координатах лапласиан выглядит на первый взгляд довольно внушительно, но при ближайшем рассмотрении оказывается конструкцией, достаточно простой. Несложные, но довольно длительные преобразования приводят к следующему выражению:
8.6. Компоненты лапласиана. Для сокращения выделим в лапласиане два слагаемых - радиальное и угловое:
Угловой оператор называется оператором Лежандра. Лапласиан приобретает сжатый вид:
8.7. Угловой оператор (оператор Лежандра) в свою очередь разделяется далее на два независимых оператора. Один действует на переменную долготы J, второй - на переменную широты j, и получается:
Операторное уравнение для оператора Лежандра встречается в нескольких очень важных фундаментальных ситуациях. Это задачи: 1) о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) об электронном строении атома H и водородоподобных ионов. 8.8. Уравнение Лапласа для сферической системы: Уравнением Лапласа называется
дифференциальное уравнение в частных производных второго порядка вида
Решения находятся по методу Фурье: для разделения переменных искомое решение представляется в виде произведения радиальной и угловой компонент функций. 8.9. Разделение переменных. Общее правило: Если в дифференциальном уравнении в частных производных можно выделить оператор, включающий несколько переменных, и привести его к аддитивной форме, придавая ему вид суммы слагаемых, определённых лишь для отдельных переменных, то исходное дифференциальное уравнение распадается на систему дифференциальных уравнений. Каждое из них и их решения определены лишь на переменных соответствующего оператора-слагаемого. Частные решения исходного дифференциального уравнения выбираются в мультипликативном виде, как произведения функций – решений отдельных уравнений системы. Этот результат сформулируем в виде краткого правила: «Оператор аддитивен-Решения мультипликативны». Этот подход встречается всюду в теории многоэлектронных систем – атомов и молекул. 8.10. Радиальная часть общего решения
сферического уравнения Лапласа выбрана в виде степенной функции от радиальной
переменной с показателем степени l принимающим одно из целочисленных
неотрицательных значений
Угловые сомножители общего решения Y(J,j) называются сферическими гармониками (шаровыми функциями). Запишем уравнение Лапласа, и рассмотрим процедуру разделения переменных:
Учитывая, что каждый из операторов активен лишь к своим переменным, получаем:
Для разделения
переменных следует слева умножить каждое из слагаемых в уравнении на
функцию, обратную искомому общему решению. Эта функция равна
8.11. Получаем равенство, обе части которого содержат независимые переменные и поэтому их обе следует приравнять постоянной величине, т.е.:
Постоянная легко определяется из радиальной части. Угловая часть уравнения Лапласа представляет собой дифференциальное уравнение Лежандра. Это второе из двух уравнений системы вида
8.12. Уравнение Лежандра Это операторное уравнение на собственные функции и собственные значения. В квантовой механике таковы все уравнения для динамических переменных. Дифференциальное уравнение Лежандра с точностью до постоянного множителя совпадает с операторным уравнением на собственные значения оператора квадрата момента импульса. Напомним, что оператор момента импульса равен
Возводя его в квадрат и вынося влево постоянный множитель, получаем:
Заменяя декартовы координаты шаровыми и производя всю последовательность действий, находим, что слева получается оператор Лежандра:
На этом основании решения уравнения Лежандра являются также и решениями операторного уравнения на собственные значения квадрата момента импульса. Так получается строгая формула квантования модуля и проекции момента импульса. 8.13. Квадрат модуля момента импульса определяется собственными значениями оператора Лежандра. Для сравнения представим оба выражения:
Допустимые значения модуля момента импульса свободно вращающейся вокруг центра масс квантовой системы (ротатора) следуют из операторного уравнения (8.15):
8.14. Уравнение Лежандра содержит две угловые переменные. Их необходимо разделить и исследовать свойства вращения. Раскрывая оператор Лежандра, получаем
Шаровые функции представим в виде Разделим переменные:
Получена система (8.18) из двух дифференциальных уравнений (8.18.1 и 8.18.2), решения которых связаны общей постоянной. 8.15. Одно из них (8.18.1) имеет знакомый вид. Оно идентично уравнению Шрёдингера для плоского ротатора и описывает свойства вращения относительно оси вращения (вдоль переменной долготы). Полное совпадение с плоским ротатором получится лишь при условии, что в атоме H это уравнение характеризует лишь часть всей ситуации и определяет проекцию момента импульса на ось вращения
Из этого уравнения вытекают значения
компоненты момента импульса вдоль оси вращения (в нашем случае – вдоль оси
аппликат): 8.16.Второе из уравнений (8.18.2) системы - дифференциальное уравнение для широты:
Наконец-то обратимся к уравнению Шрёдингера для водородоподобного атома! 8.17. Гамильтониан и уравнение Шрёдингера
8.17. Несложные преобразования, состоящие только в перемещении и группировке слагаемых, дают следующее:
Уравнение Шрёдингера для атома водорода приведено к компактному операторному виду, и здесь уже возможно его решение по методу Фурье разделения переменных. Решения содержат радиальный и угловой сомножители:
8.18. Схема разделения переменных та же, что и в уравнении Лапласа (по правилу «оператор аддитивен - решение мультипликативно». Есть сомножитель радиальный, и есть угловой, и частные решения углового уравнения – сферические функции. Разделим переменные:
Получается система (8.29) из двух дифференциальных уравнений: (8.29.1) - уравнение Лежандра для сферических гармоник (с точностью до постоянной совпадающее с уравнением для квадрата модуля момента импульса !), и (8.29.2) - чисто радиальное:
8.19.1. Гамильтониан для электрона в водородоподобном ионе (атоме):
8.19.2. Лапласиан в сферических переменных:
8.19.3. Уравнение Шрёдингера
Потенциальная функция V(r) имеет вид: 1) у атома H V(r) = -e2/r, 2) у водородоподобного иона V(r) =-Ze2/r. Уравнение Шрёдингера в общем виде для водородоподобного иона приобретает вид
Оно разделяется на систему из трёх дифференциальных уравнений:
От потенциала зависит лишь радиальная, но не угловая часть уравнения Шрёдингера. Система этих уравнений даёт полное описание атомных орбиталей - одноэлектронных волновых функций в простейшем случае – в водородоподобном ионе. Первое уравнение совпадает с уравнением Шрёдингера для плоского ротатора, оно описывает свойства вращения вокруг аппликаты (мы выполняли преобразования так, что это ось z). Решения этого уравнения нумеруются квантовым числом
1) Первое уравнение (как и в плоском ротаторе) описывает компоненту момента импульса вдоль оси вращения, определяя проекцию вектора момента с помощью квантового числа m. 2) Второе и первое уравнения вместе (до разделения угловых переменных) проистекают из одного общего дифференциального уравнения Лежандра
из которого следует правило квантования модуля момента импульса с помощью числа l :
Уравнение (E) предписывает условие
и возникает следствие 3) Радиальное уравнение приводит к квантованию энергии электронного уровня. Правило квантования одноэлектронных уровней – энергетический спектр водородоподобного иона выражается формулой Бора:
В итоге каждую из атомных орбиталей в
атоме водорода можно быть охарактеризовать (пронумеровать) тройкой квантовых
чисел 8.20.1. Квантовые числа, интервалы возможных значений. 8.20.2. Водородоподобные атомные орбитали. Угловые компоненты АО и распределение вероятностей. Полярные функции азимута Qlm(J) и функций широты F|m|(j)
Полярные диаграммы функций азимута Qlm(J) и функций широты F|m|(j). Радиальные компоненты АО атома Н и их графики. Радиальное распределение плотности вероятности и квантово-химический смысл боровского радиуса.
= Z(r/a0) 8.20.1. Квантовые числа, интервалы возможных значений. 8.20.3. Пространственные размеры атома водорода. 8.20.4. Наиболее вероятное удаление электрона от ядра. (Радиус наибольшей плотности вероятности)
Радиус максимальной плотности вероятности называется боровским радиусом и совпадает с радиусом первой орбиты в теории атома водорода по Бору. 8.20.5.Среднее расстояние электрона от ядра. Поскольку АО представляет собою нормированную одноэлектронную волновую функцию, то знаменатель в формуле для среднего значения любой физической величины, в том числе и расстояния электрона от ядра можно не выписывать, он равен единице, и отсюда следует:
Среднее расстояние электрона от ядра в полтора раза больше наиболее вероятного - боровского радиуса. Примечание. Использован вспомогательный
интеграл: (См. теорию Эйлера Гамма - функции 1-го рода). Энергетическая диаграмма уровней АО атома Н и Z-1–зарядного водородоподобного иона приводится ниже, где она качественные сравнивается со схемой уровней многоэлектронного атома. |
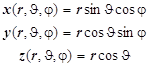
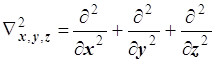 . (8.2)
. (8.2)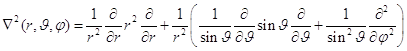 . (8.3)
. (8.3)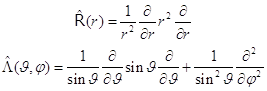 (8.4)
(8.4)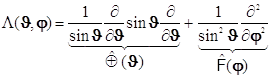
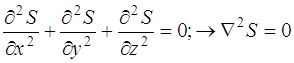 . В сферических переменных
оно имеет вид
. В сферических переменных
оно имеет вид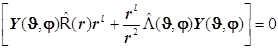 . (8.11)
. (8.11)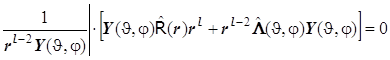
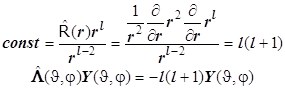 .
(8.13)
.
(8.13)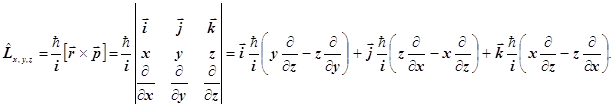
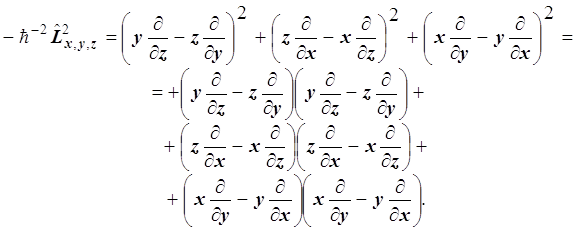
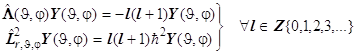 . (8.15)
. (8.15)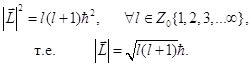 . (8.16)
. (8.16)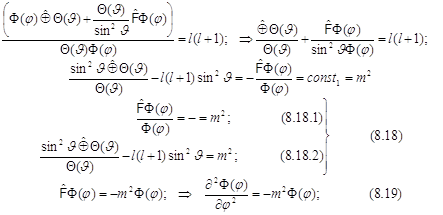
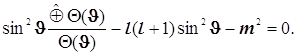 (8.22)
(8.22)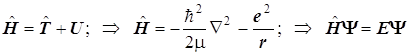 . (8.23)
. (8.23)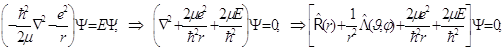
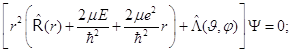 ()
()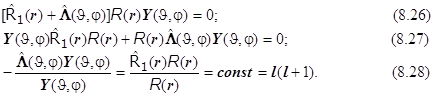
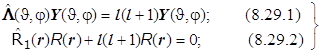 . (8.29)8.19. Итоги.
. (8.29)8.19. Итоги.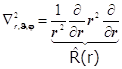 +
+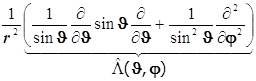
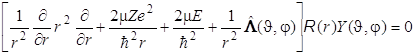 . (8.33)
. (8.33)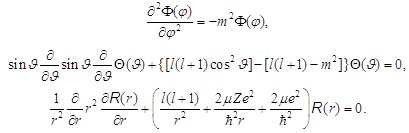 . (8.34)
. (8.34)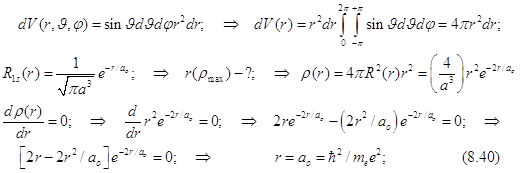
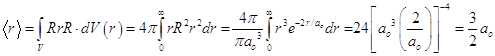 . (8.41)
. (8.41)